题目内容
已知 的展开式的二项式系数和比(3x-2)n的展开式的系数和大1023.求
的展开式的二项式系数和比(3x-2)n的展开式的系数和大1023.求 的展开式中:
的展开式中:(1)二项式系数最大的项;(2)系数的绝对值最大的项.
【答案】分析:(1)对x进行赋值,令x=1,即可得到关于n的方程,求出n,根据二项式系数的性质即可求出二项式系数最大的项
(2)设出第r+1项为系数的绝对值最大的项,即可列出关于r的不等式 ,即可求解
,即可求解
解答:解:由题意可得, 的展开式的二项式系数和22n,
的展开式的二项式系数和22n,
在(3x-2)n中,令x=1可得展开式的系数和为1
∴22n-1=1023
∴n=5, 的展开式的通项
的展开式的通项 =
=
(1)当n=5时2n=10, 的展开式中共有11项,二项式系数最大项为r=5时,即第6项,
的展开式中共有11项,二项式系数最大项为r=5时,即第6项,
(2)要求 的展开式中系数的绝对值最大的项,只要求
的展开式中系数的绝对值最大的项,只要求 展开式中系数最大的值
展开式中系数最大的值
由 ,
,
∴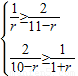 ,解不等式组可得
,解不等式组可得
∴r=3
 =
=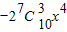
点评:本题通过赋值法求出n,根据二项式系数的性质,同时利用展开式的通项进行求解,属于中档题.
(2)设出第r+1项为系数的绝对值最大的项,即可列出关于r的不等式
 ,即可求解
,即可求解解答:解:由题意可得,
 的展开式的二项式系数和22n,
的展开式的二项式系数和22n,在(3x-2)n中,令x=1可得展开式的系数和为1
∴22n-1=1023
∴n=5,
 的展开式的通项
的展开式的通项 =
=
(1)当n=5时2n=10,
 的展开式中共有11项,二项式系数最大项为r=5时,即第6项,
的展开式中共有11项,二项式系数最大项为r=5时,即第6项,
(2)要求
 的展开式中系数的绝对值最大的项,只要求
的展开式中系数的绝对值最大的项,只要求 展开式中系数最大的值
展开式中系数最大的值由
 ,
,∴
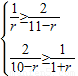 ,解不等式组可得
,解不等式组可得
∴r=3
 =
=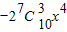
点评:本题通过赋值法求出n,根据二项式系数的性质,同时利用展开式的通项进行求解,属于中档题.

练习册系列答案
相关题目
 的展开式的二项式系数之和为32,则展开式中含
的展开式的二项式系数之和为32,则展开式中含 项的系数是( )
项的系数是( ) 的展开式的二项式系数和比
的展开式的二项式系数和比 的展开式的系数和大992,求
的展开式的系数和大992,求 的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。
的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。 的展开式中,第5项的系数与第3项的系数比是10:1
的展开式中,第5项的系数与第3项的系数比是10:1 的项
的项