ЬтФПФкШн
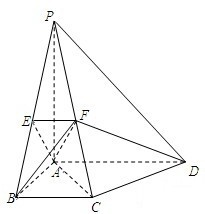 ЃЈ2013•ГЏбєЧјвЛФЃЃЉШчЭМЃЌдкЫФРтзЖP-ABCDжаЃЌЦНУцPACЁЭЦНУцABCDЃЌЧвPAЁЭACЃЌPA=AD=2ЃЎЫФБпаЮABCDТњзуBCЁЮADЃЌABЁЭADЃЌAB=BC=1ЃЎЕуEЃЌFЗжБ№ЮЊВрРтPBЃЌPCЩЯЕФЕуЃЌЧв
ЃЈ2013•ГЏбєЧјвЛФЃЃЉШчЭМЃЌдкЫФРтзЖP-ABCDжаЃЌЦНУцPACЁЭЦНУцABCDЃЌЧвPAЁЭACЃЌPA=AD=2ЃЎЫФБпаЮABCDТњзуBCЁЮADЃЌABЁЭADЃЌAB=BC=1ЃЎЕуEЃЌFЗжБ№ЮЊВрРтPBЃЌPCЩЯЕФЕуЃЌЧв| PE |
| PB |
| PF |
| PC |
ЃЈЂёЃЉЧѓжЄЃКEFЁЮЦНУцPADЃЛ
ЃЈЂђЃЉЕБІЫ=
| 1 |
| 2 |
ЃЈЂѓЃЉЪЧЗёДцдкЪЕЪ§ІЫЃЌЪЙЕУЦНУцAFDЁЭЦНУцPCDЃПШєДцдкЃЌЪдЧѓГіІЫЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЗжЮіЃКЃЈЂёЃЉгЩ
=
=ІЫПЩжЊЃЌEFЁЮBCЃЌвРЬтвтЃЌПЩЧѓЕУEFЁЮADЃЌдйРћгУЯпУцЦНааЕФХаЖЯЖЈРэМДПЩжЄЕУНсТлЃЛ
ЃЈЂђЃЉПЩжЄЕУPAЃЌABЃЌADСНСНДЙжБЃЌвджЎЮЊжсНЈСЂПеМфжБНЧзјБъЯЕЃЌПЩЧѓЕУ
гы
ЕФзјБъЃЌРћгУЯђСПЕФЪ§СПЛ§МДПЩЧѓЕУвьУцжБЯпBFгыCDЫљГЩНЧЕФгрЯвжЕЃЛ
ЃЈЂѓЃЉЩшFЃЈx0ЃЌy0ЃЌz0ЃЉЃЌдђ
=ЃЈx0ЃЌy0ЃЌz0-2ЃЉЃЌ
=ЃЈ1ЃЌ1ЃЌ-2ЃЉЃЌгЩ
=ІЫ
ЃЌПЩЧѓЕУFЃЈІЫЃЌІЫЃЌ2-2ІЫЃЉЃЌдйЩшГіЦНУцAFDЕФвЛИіЗЈЯђСПЮЊn1=ЃЈx1ЃЌy1ЃЌz1ЃЉЃЌЦНУцPCDЕФвЛИіЗЈЯђСПЮЊn2=ЃЈx2ЃЌy2ЃЌz2ЃЉЃЌПЩЧѓЕУетСНИіЗЈЯђСПЕФзјБъЃЌРћгУn1•n2=0ЃЌМДПЩЧѓЕУІЫЕФжЕЃЎ
| PE |
| PB |
| PF |
| PC |
ЃЈЂђЃЉПЩжЄЕУPAЃЌABЃЌADСНСНДЙжБЃЌвджЎЮЊжсНЈСЂПеМфжБНЧзјБъЯЕЃЌПЩЧѓЕУ
| BF |
| CD |
ЃЈЂѓЃЉЩшFЃЈx0ЃЌy0ЃЌz0ЃЉЃЌдђ
| PF |
| PC |
| PF |
| PC |
НтД№ЃК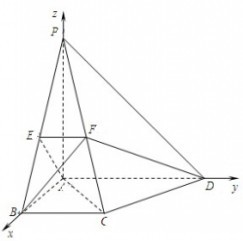 жЄУїЃКЃЈЂёЃЉгЩвбжЊЃЌ
жЄУїЃКЃЈЂёЃЉгЩвбжЊЃЌ
=
=ІЫЃЌ
ЫљвдEFЁЮBCЃЎ
вђЮЊBCЁЮADЃЌЫљвдEFЁЮADЃЎ
ЖјEF?ЦНУцPADЃЌAD?ЦНУцPADЃЌ
ЫљвдEFЁЮЦНУцPADЃЎ ЁЃЈ4ЗжЃЉ
ЃЈЂђЃЉвђЮЊЦНУцABCDЁЭЦНУцPACЃЌ
ЦНУцABCDЁЩЦНУцPAC=ACЃЌЧвPAЁЭACЃЌ
ЫљвдPAЁЭЦНУцABCDЃЎ
ЫљвдPAЁЭABЃЌPAЁЭADЃЎ
гжвђЮЊABЁЭADЃЌ
ЫљвдPAЃЌABЃЌADСНСНДЙжБЃЎ ЁЃЈ5ЗжЃЉ
ШчЭМЫљЪОЃЌНЈСЂПеМфжБНЧзјБъЯЕЃЌ
вђЮЊAB=BC=1ЃЌPA=AD=2ЃЌ
ЫљвдAЃЈ0ЃЌ0ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЌ0ЃЉЃЌCЃЈ1ЃЌ1ЃЌ0ЃЉЃЌDЃЈ0ЃЌ2ЃЌ0ЃЉЃЌPЃЈ0ЃЌ0ЃЌ2ЃЉЃЎ
ЕБІЫ=
ЪБЃЌFЮЊPCжаЕуЃЌ
ЫљвдFЃЈ
ЃЌ
ЃЌ1ЃЉЃЌ
Ыљвд
=ЃЈ-
ЃЌ
ЃЌ1ЃЉЃЌ
=ЃЈ-1ЃЌ1ЃЌ0ЃЉЃЎ
ЩшвьУцжБЯпBFгыCDЫљГЩЕФНЧЮЊІШЃЌ
ЫљвдcosІШ=|cosЃМ
ЃЌ
ЃО|=
=
ЃЌ
ЫљвдвьУцжБЯпBFгыCDЫљГЩНЧЕФгрЯвжЕЮЊ
ЃЎЁЃЈ9ЗжЃЉ
ЃЈЂѓЃЉЩшFЃЈx0ЃЌy0ЃЌz0ЃЉЃЌдђ
=ЃЈx0ЃЌy0ЃЌz0-2ЃЉЃЌ
=ЃЈ1ЃЌ1ЃЌ-2ЃЉЃЎ
гЩвбжЊ
=ІЫ
ЃЌЫљвдЃЈx0ЃЌy0ЃЌz0-2ЃЉ=ІЫЃЈ1ЃЌ1ЃЌ-2ЃЉЃЌ
Ыљвд
ЃЌ
Ёр
=ЃЈІЫЃЌІЫЃЌ2-2ІЫЃЉЃЎ
ЩшЦНУцAFDЕФвЛИіЗЈЯђСПЮЊn1=ЃЈx1ЃЌy1ЃЌz1ЃЉЃЌвђЮЊ
=ЃЈ0ЃЌ2ЃЌ0ЃЉЃЌ
Ыљвд
МД
ЃЌ
Сюz1=ІЫЃЌЕУn1=ЃЈ2ІЫ-2ЃЌ0ЃЌІЫЃЉЃЎ
ЩшЦНУцPCDЕФвЛИіЗЈЯђСПЮЊn2=ЃЈx2ЃЌy2ЃЌz2ЃЉЃЌ
вђЮЊ
=ЃЈ0ЃЌ2ЃЌ-2ЃЉЃЌ
=ЃЈ-1ЃЌ1ЃЌ0ЃЉЃЌ
Ыљвд
МД
Сюx2=1ЃЌдђn2=ЃЈ1ЃЌ1ЃЌ1ЃЉЃЎ
ШєЦНУцAFDЁЭЦНУцPCDЃЌдђn1•n2=0ЃЌЫљвдЃЈ2ІЫ-2ЃЉ+ІЫ=0ЃЌНтЕУІЫ=
ЃЎ
ЫљвдЕБІЫ=
ЪБЃЌЦНУцAFDЁЭЦНУцPCDЃЎЁЃЈ14ЗжЃЉ
 жЄУїЃКЃЈЂёЃЉгЩвбжЊЃЌ
жЄУїЃКЃЈЂёЃЉгЩвбжЊЃЌ| PE |
| PB |
| PF |
| PC |
ЫљвдEFЁЮBCЃЎ
вђЮЊBCЁЮADЃЌЫљвдEFЁЮADЃЎ
ЖјEF?ЦНУцPADЃЌAD?ЦНУцPADЃЌ
ЫљвдEFЁЮЦНУцPADЃЎ ЁЃЈ4ЗжЃЉ
ЃЈЂђЃЉвђЮЊЦНУцABCDЁЭЦНУцPACЃЌ
ЦНУцABCDЁЩЦНУцPAC=ACЃЌЧвPAЁЭACЃЌ
ЫљвдPAЁЭЦНУцABCDЃЎ
ЫљвдPAЁЭABЃЌPAЁЭADЃЎ
гжвђЮЊABЁЭADЃЌ
ЫљвдPAЃЌABЃЌADСНСНДЙжБЃЎ ЁЃЈ5ЗжЃЉ
ШчЭМЫљЪОЃЌНЈСЂПеМфжБНЧзјБъЯЕЃЌ
вђЮЊAB=BC=1ЃЌPA=AD=2ЃЌ
ЫљвдAЃЈ0ЃЌ0ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЌ0ЃЉЃЌCЃЈ1ЃЌ1ЃЌ0ЃЉЃЌDЃЈ0ЃЌ2ЃЌ0ЃЉЃЌPЃЈ0ЃЌ0ЃЌ2ЃЉЃЎ
ЕБІЫ=
| 1 |
| 2 |
ЫљвдFЃЈ
| 1 |
| 2 |
| 1 |
| 2 |
Ыљвд
| BF |
| 1 |
| 2 |
| 1 |
| 2 |
| CD |
ЩшвьУцжБЯпBFгыCDЫљГЩЕФНЧЮЊІШЃЌ
ЫљвдcosІШ=|cosЃМ
| BF |
| CD |
|(-
| ||||||||
|
| ||
| 3 |
ЫљвдвьУцжБЯпBFгыCDЫљГЩНЧЕФгрЯвжЕЮЊ
| ||
| 3 |
ЃЈЂѓЃЉЩшFЃЈx0ЃЌy0ЃЌz0ЃЉЃЌдђ
| PF |
| PC |
гЩвбжЊ
| PF |
| PC |
Ыљвд
|
Ёр
| AF |
ЩшЦНУцAFDЕФвЛИіЗЈЯђСПЮЊn1=ЃЈx1ЃЌy1ЃЌz1ЃЉЃЌвђЮЊ
| AD |
Ыљвд
|
|
Сюz1=ІЫЃЌЕУn1=ЃЈ2ІЫ-2ЃЌ0ЃЌІЫЃЉЃЎ
ЩшЦНУцPCDЕФвЛИіЗЈЯђСПЮЊn2=ЃЈx2ЃЌy2ЃЌz2ЃЉЃЌ
вђЮЊ
| PD |
| CD |
Ыљвд
|
|
Сюx2=1ЃЌдђn2=ЃЈ1ЃЌ1ЃЌ1ЃЉЃЎ
ШєЦНУцAFDЁЭЦНУцPCDЃЌдђn1•n2=0ЃЌЫљвдЃЈ2ІЫ-2ЃЉ+ІЫ=0ЃЌНтЕУІЫ=
| 2 |
| 3 |
ЫљвдЕБІЫ=
| 2 |
| 3 |
ЕуЦРЃКБОЬтПМВщжБЯпгыЦНУцЕФЦНааЃЌПМВщвьУцжБЯпЫљГЩЕФНЧЃЌПМВщУцУцДЙжБЃЌЭЛГіПМВщПеМфжБНЧзјБъЯЕдкжЄУїгыМЦЫужаЕФгІгУЃЎЪєгкжаЕЕЬтЃЎ

СЗЯАВсЯЕСаД№АИ
 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
ЯрЙиЬтФП
