题目内容
四棱锥P-ABCD中,底面ABCD是平行四边形, =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1),则PA与底面ABCD的关系是
=(-1,2,-1),则PA与底面ABCD的关系是
- A.相交
- B.垂直
- C.不垂直
- D.成60°角
B
分析:由已知中向量 =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
=(-1,2,-1),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
解答:证明:(1)∵ =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1),
=(-1,2,-1),
∴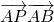 =-1×2+2×(-1)+(-1)×(-4)=0,同样
=-1×2+2×(-1)+(-1)×(-4)=0,同样 =0,
=0,
∴AP⊥AB,AP⊥AD,
即AP⊥AB且AP⊥AD,
又∵AB∩AD=A
∴AP⊥平面ABCD;
故选B.
点评:本题考查的知识点是向量表述线线垂直的关系,空间点到点距离的运算,其中证得AP⊥AB且AP⊥AD是关键.
分析:由已知中向量
 =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;
=(-1,2,-1),根据两个向量的数量积为0,两个向量垂直,我们可以判断出AP⊥AB且AP⊥AD,进而根据线面垂直的判定定理得到PA⊥底面ABCD;解答:证明:(1)∵
 =(2,-1,-4),
=(2,-1,-4), =(4,2,0),
=(4,2,0), =(-1,2,-1),
=(-1,2,-1),∴
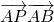 =-1×2+2×(-1)+(-1)×(-4)=0,同样
=-1×2+2×(-1)+(-1)×(-4)=0,同样 =0,
=0,∴AP⊥AB,AP⊥AD,
即AP⊥AB且AP⊥AD,
又∵AB∩AD=A
∴AP⊥平面ABCD;
故选B.
点评:本题考查的知识点是向量表述线线垂直的关系,空间点到点距离的运算,其中证得AP⊥AB且AP⊥AD是关键.

练习册系列答案
相关题目
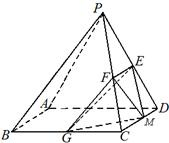 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PD、PC、BC的中点.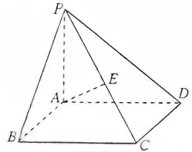 (2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2
(2012•上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2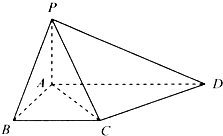 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,且AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD,若PA=AB=BC= 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点.
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°,M为AB的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,其中PA=PD=AD=2,∠BAD=60°,Q为AD的中点.