题目内容
(本小题满分l2分)
设椭圆
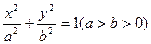 的焦点分别为
的焦点分别为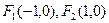 ,直线
,直线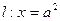 交
交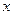 轴于点
轴于点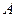 ,且
,且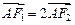 .
.(Ⅰ)试求椭圆的方程;
(Ⅱ)过
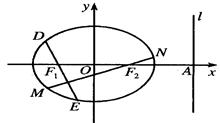
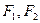 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形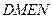 面积的最大值和最小值.
面积的最大值和最小值.
|
解:(1)由题意,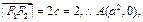
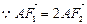
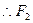 为
为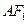 的中点
的中点
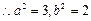
即:椭圆方程为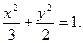 …………………(6分)
…………………(6分)
(2)当直线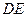 与
与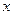 轴垂直时,
轴垂直时,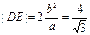 ,此时
,此时 ,四边形
,四边形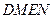 的面积
的面积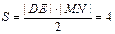 .同理当
.同理当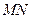 与
与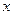 轴垂直时,也有四边形
轴垂直时,也有四边形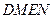 的面积
的面积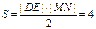 .当直线
.当直线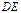 ,
, 均与
均与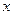 轴不垂直时,设
轴不垂直时,设 :
: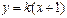 ,代入消去
,代入消去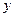 得:
得: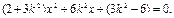 设
设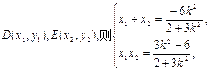
∴,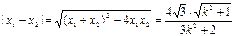 ,所以,
,所以,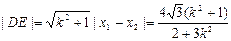 ,
,
同理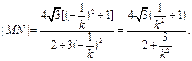 ∴四边形的面积
∴四边形的面积
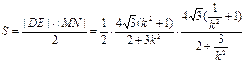
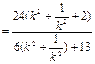
令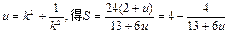 因为
因为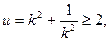 当
当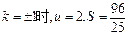 ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以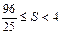
综上可知, .故
.故 四边形
四边形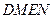 面积的最大值为4,最小值为
面积的最大值为4,最小值为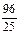 .…(12分)
.…(12分)
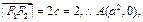
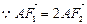
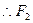 为
为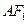 的中点
的中点 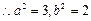
即:椭圆方程为
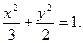 …………………(6分)
…………………(6分)(2)当直线
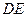 与
与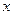 轴垂直时,
轴垂直时,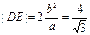 ,此时
,此时 ,四边形
,四边形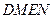 的面积
的面积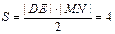 .同理当
.同理当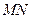 与
与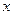 轴垂直时,也有四边形
轴垂直时,也有四边形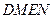 的面积
的面积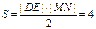 .当直线
.当直线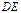 ,
, 均与
均与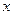 轴不垂直时,设
轴不垂直时,设 :
: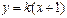 ,代入消去
,代入消去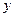 得:
得: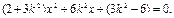 设
设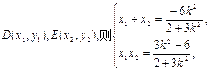
∴,
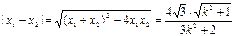 ,所以,
,所以,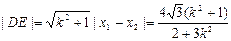 ,
,同理
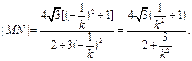 ∴四边形的面积
∴四边形的面积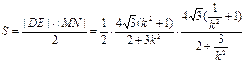
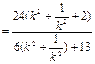
令
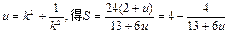 因为
因为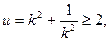 当
当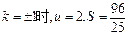 ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以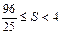
综上可知,
 .故
.故 四边形
四边形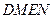 面积的最大值为4,最小值为
面积的最大值为4,最小值为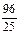 .…(12分)
.…(12分)略

练习册系列答案
相关题目
 是椭圆
是椭圆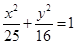 上的点.若
上的点.若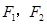 是椭圆的两个焦点,则
是椭圆的两个焦点,则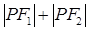 等于( )
等于( )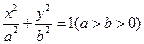 的左、右焦点为
的左、右焦点为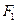 、
、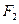 ,离心率为
,离心率为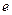 。直线
。直线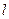 :
: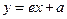 与
与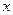 轴、
轴、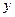 轴分别交于点A、B,M是直线
轴分别交于点A、B,M是直线 椭圆C的一个公共点,P是点
椭圆C的一个公共点,P是点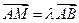 。
。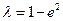
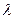 的值,使得
的值,使得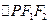 是等腰三角形。
是等腰三角形。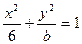 (
(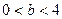 ),抛物线方程为
),抛物线方程为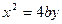 .过抛物线的焦点作
.过抛物线的焦点作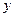 轴的垂线,与抛物线在第一象限的交点为
轴的垂线,与抛物线在第一象限的交点为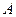 ,抛物线在点
,抛物线在点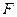 .
. 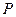 为椭圆上的动点,由
为椭圆上的动点,由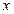 轴作垂线
轴作垂线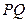 ,垂足为
,垂足为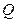 ,且直线
,且直线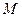 满足
满足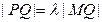 ,求点
,求点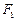 、
、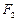 是椭圆
是椭圆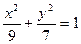 的两个焦点,
的两个焦点,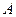 为椭圆上一点,且∠
为椭圆上一点,且∠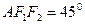 ,则
,则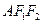 的面积为( )
的面积为( )
 B
B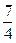 C
C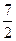 D
D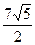
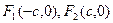 为椭圆
为椭圆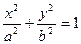 的两个焦点,P为椭圆上一点且
的两个焦点,P为椭圆上一点且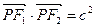 ,则此椭圆离心率的取值范围是 ( ▲ )
,则此椭圆离心率的取值范围是 ( ▲ )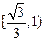
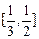
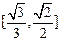
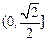
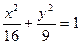 的焦距是 ,焦点坐标为 ;若CD为过左焦点
的焦距是 ,焦点坐标为 ;若CD为过左焦点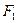 的弦,则
的弦,则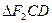 的周长为
的周长为
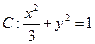 的两个焦点为
的两个焦点为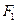 、
、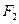 ,点
,点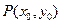 满足
满足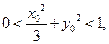 则
则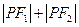 的取值范围为 ,直线
的取值范围为 ,直线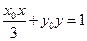 与椭圆
与椭圆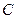 的公共点的个数为
的公共点的个数为 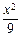 +
+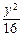 =1的两焦点为F1、F2,点P在椭圆上,且直线PF1、PF2的夹角为
=1的两焦点为F1、F2,点P在椭圆上,且直线PF1、PF2的夹角为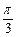 ,则△PF1F2的面积为
,则△PF1F2的面积为