题目内容
在三棱锥P-ABC中，△PAB、△PBC、△PAC、△ABC中是直角三角形的最多有（ ）
分析：在三棱锥P-ABC中，底面ABC是直角三角形，且∠C=90°，PA⊥平面ABC，由三垂线定理，知△PAB、△PBC、△PAC、△ABC都是直角三角形．
解答：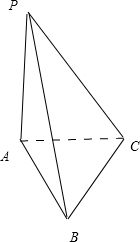
解：如图，在三棱锥P-ABC中，
底面ABC是直角三角形，
且∠C=90°，
PA⊥平面ABC，
由三垂线定理，
很容易知道，△PAB、△PBC、△PAC、△ABC都是直角三角形．
故选D．
解：如图，在三棱锥P-ABC中，底面ABC是直角三角形，
且∠C=90°，
PA⊥平面ABC，
由三垂线定理，
很容易知道，△PAB、△PBC、△PAC、△ABC都是直角三角形．
故选D．
点评：本题考查棱锥的结构特征，是基础题．解题时要认真审题，仔细解答，注意三垂线定理的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在三棱锥P-ABC中，
在三棱锥P-ABC中，AB=3，BC=4，AC=5，PA=1 面PAB⊥面CAB，面PAC⊥面CAB，则三棱锥P-ABC的体积是（ ）
在三棱锥P-ABC中，PA⊥平面ABC．
（2013•蚌埠二模）如图，在三棱锥P-ABC中，PA=PB=AB=2，BC=3，∠ABC=90°，平面PAB⊥平面ABC，D，E分别为AB，AC中点．