题目内容
给出下列命题:
(1)存在实数α使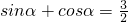 .
.
(2)直线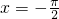 是函数y=sinx图象的一条对称轴.
是函数y=sinx图象的一条对称轴.
(3)y=cos(cosx)(x∈R)的值域是[cos1,1].
(4)若α,β都是第一象限角,且α>β,则tanα>tanβ.
其中正确命题的题号为
- A.(1)(2)
- B.(2)(3)
- C.(3)(4)
- D.(1)(4)
B
分析:(1)利用辅助角公式将 可判断(1);
可判断(1);
(2)根据函数y=sinx图象的对称轴方程可判断(2);
(3)根据余弦函数的性质可求出y=cos(cosx)(x∈R)的最大值与最小值,从而可判断(3)的正误;
(4)用特值法令α,β都是第一象限角,且α>β,可判断(4).
解答:(1)∵ ,∴(1)错误;
,∴(1)错误;
(2)∵y=sinx图象的对称轴方程为 ,k=-1,
,k=-1,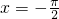 ,∴(2)正确;
,∴(2)正确;
(3)根据余弦函数的性质可得y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
(4)不妨令 ,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
故选B.
点评:本题考查正弦函数与余弦函数、正切函数的性质,着重考查学生综合运用三角函数的性质分析问题、解决问题的能力,属于中档题.
分析:(1)利用辅助角公式将
 可判断(1);
可判断(1);(2)根据函数y=sinx图象的对称轴方程可判断(2);
(3)根据余弦函数的性质可求出y=cos(cosx)(x∈R)的最大值与最小值,从而可判断(3)的正误;
(4)用特值法令α,β都是第一象限角,且α>β,可判断(4).
解答:(1)∵
 ,∴(1)错误;
,∴(1)错误;(2)∵y=sinx图象的对称轴方程为
 ,k=-1,
,k=-1,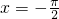 ,∴(2)正确;
,∴(2)正确;(3)根据余弦函数的性质可得y=cos(cosx)的最大值为ymax=cos0=1,ymin=cos(cos1),其值域是[cos1,1],(3)正确;
(4)不妨令
 ,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;
,满足α,β都是第一象限角,且α>β,但tanα<tanβ,(4)错误;故选B.
点评:本题考查正弦函数与余弦函数、正切函数的性质,着重考查学生综合运用三角函数的性质分析问题、解决问题的能力,属于中档题.

练习册系列答案
相关题目