题目内容
在△ABC中，设A、B、C的对边分别为a、b、c，向量m=(cosA,sinA),n=(
-sinA,cosA),若|m+n|=2.
（1）求角A的大小；
（2）若b=4,且c=a，求△ABC的面积.
-sinA,cosA),若|m+n|=2.（1）求角A的大小；
（2）若b=4
,且c=a，求△ABC的面积.（1）A=
（2）16
（2）16（1）m+n=(+cosA-sinA,cosA+sinA)
|m+n|2=(+cosA-sinA)2+(cosA+sinA)2
=2+2(cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2
=2+2(cosA-sinA)+2
=4-4sin（A-）
∵|m+n|=2,∴4-4sin（A-）=4,sin（A-）=0.
又∵0＜A＜
,∴-＜A-＜
,∴A-=0,
∴A=.
(2)由余弦定理，a2=b2+c2-2bccosA,
又b=4,c=a,A=，
得a2=32+2a2-2×4×a·
,
即a2-8a+32=0,解得a=4，∴c=8.
∴S△ABC=
b·csinA=×4×8×sin=16.
S△ABC=×(4)2=16.
+cosA-sinA,cosA+sinA)|m+n|2=(
+cosA-sinA)2+(cosA+sinA)2=2+2
(cosA-sinA)+(cosA-sinA)2+(cosA+sinA)2=2+2
(cosA-sinA)+2=4-4sin（A-
）∵|m+n|=2,∴4-4sin（A-
）=4,sin（A-）=0.又∵0＜A＜
,∴-＜A-＜,∴A-=0,∴A=
.(2)由余弦定理，a2=b2+c2-2bccosA,
又b=4
,c=a,A=，得a2=32+2a2-2×4
×a·,即a2-8
a+32=0,解得a=4，∴c=8.∴S△ABC=
b·csinA=×4×8×sin=16.S△ABC=
×(4)2=16.
练习册系列答案
开心蛙口算题卡系列答案
相关题目
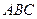中，角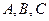
所对的边分别为
，
．
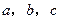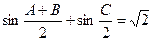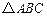
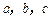
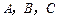
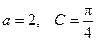
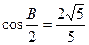
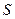
中，
，且
，求
．
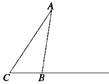求AC的长度越短越好，求AC最短为多少米？且当AC最短时，BC长度为多少米？
中角A、B、C的对边，
，
，D是边BA延长线上的点，且AD
．
的值；
的大小．
中，
分别是角A、B、C的对边，且
.
；（II）若
，求
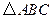中，若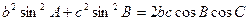
，试判断三角形的形状．