题目内容
已知函数h(x),定义fk(x)=h(x-mk)+nk,x∈(mk,m+mk],k∈Z(其中m>0、n>0是常数)叫阶梯函数的第k阶,m叫阶宽,n叫阶高.
(1)若h(x)=2x,求当阶宽为2,阶高为3的第0阶和第k函数f0(x)和fk(x)的解析式;
(2)若h(x)=x2,设阶宽为2,阶高为3;是否存在正整数k,使得fk(x)<(1-3k)x+4k2+3k-1有解?
(1)若h(x)=2x,求当阶宽为2,阶高为3的第0阶和第k函数f0(x)和fk(x)的解析式;
(2)若h(x)=x2,设阶宽为2,阶高为3;是否存在正整数k,使得fk(x)<(1-3k)x+4k2+3k-1有解?
(1)f0(x)=h(x)=2x,x∈(0,2];fk(x)=h(x-2k)+3k=2 x-2k+3k,x∈(2k,2k+2],k∈Z.
(2)若h(x)=x2,则fk(x)=(x-2k)2+3k,fk(x)<(1-3k)x+4k2+3k-1
?(x-2k)2+3k<(1-3k)x+4k2+3k-1,
整理得出x2-(k+1)x+1<0.
当k=1时,x2-2x+1<0无解,当k≥2时,x2-(k+1)x+1<0,
得出
<x<
①
又根据x∈(2k,2k+2],k∈Z ②
又根据
<
=k+1<2k,
①②无公共部分,即不存在正整数k满足题意.
(2)若h(x)=x2,则fk(x)=(x-2k)2+3k,fk(x)<(1-3k)x+4k2+3k-1
?(x-2k)2+3k<(1-3k)x+4k2+3k-1,
整理得出x2-(k+1)x+1<0.
当k=1时,x2-2x+1<0无解,当k≥2时,x2-(k+1)x+1<0,
得出
k+1-
| ||
| 2 |
k+1+
| ||
| 2 |
又根据x∈(2k,2k+2],k∈Z ②
又根据
k+1+
| ||
| 2 |
k+1+
| ||
| 2 |
①②无公共部分,即不存在正整数k满足题意.

练习册系列答案
相关题目
 x3+
x3+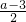 x2+(a2-3a)x-2a
x2+(a2-3a)x-2a [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明. x3+
x3+ x2+(a2-3a)x-2a
x2+(a2-3a)x-2a [g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.
[g(x)-27],m,n∈(0,1)且m≠n,试比较|H(m)-H(n)|与|em-en|(e为自然对数的底)的大小,并证明.