题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{1,0≤x≤1}\\{3-x,x<0或x>1}\end{array}\right.$,若f[f(x)]=1,则实数x的取值范围是[0,1]∪[2,3].分析 利用分段函数直接判断x的范围,求解即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{1,0≤x≤1}\\{3-x,x<0或x>1}\end{array}\right.$,f[f(x)]=1,
当x∈[0,1]时,f[f(x)]=1恒成立.
当x<0时,f(x)=3-x>3,可得3-(3-x)=1,不成立;
当x>1时,f(x)=3-x,
若1<3-x≤2.即x∈[1,2),可得3-(3-x)=1,不成立;
若0≤3-x≤1即x∈[2,3]时,f[f(x)]=1,恒成立.
若3-x<0,即x>3时,可得3-(3-x)=1,不成立;
综上x∈[0,1]∪[2,3].
故答案为:[0,1]∪[2,3].
点评 本题考查分段函数的应用,考查分类讨论以及计算能力.

练习册系列答案
相关题目
10.在集合{1,2,3,4}中任取一个偶数a和一个奇数b构成以原点为起点的向量$\overrightarrow{α}$=(a,b).从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形.记所有作成的平行四边形的个数为n,其中面积不超过4的平行四边形的个数为m,则$\frac{m}{n}$=( )
| A. | $\frac{4}{15}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{5}$ | D. | $\frac{2}{3}$ |
5.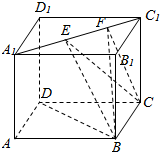 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | BD⊥CE | |
| B. | △CEF的面积为定值 | |
| C. | 四面体BCEF的体积随EF的位置的变化而变化 | |
| D. | 直线BE与CF为异面直线 |
9.已知sinα+cosα=$\frac{1}{2}$,α∈(0,π),则$\frac{1-tanα}{1+tanα}$=( )
| A. | $\sqrt{7}$ | B. | -$\sqrt{7}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |