题目内容
6.△ABC外接圆的半径为2,圆心为O,且2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,则$\overrightarrow{CA}$•$\overrightarrow{CB}$的值是( )| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
分析 运用向量的三角形法则,以及外心的特点,可得O为BC的中点,A为直角,再由勾股定理和向量的数量积的定义,计算即可得到.
解答  解:2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,即有2$\overrightarrow{OA}$+$\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$=$\overrightarrow{0}$,
解:2$\overrightarrow{OA}$+$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{0}$,即有2$\overrightarrow{OA}$+$\overrightarrow{OB}$-$\overrightarrow{OA}$+$\overrightarrow{OC}$-$\overrightarrow{OA}$=$\overrightarrow{0}$,
可得$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,则O为BC的中点,
即有AB⊥AC,
又|$\overrightarrow{OA}$|=|$\overrightarrow{AB}$|,
则△ABO为等边三角形,且边长为2,
由勾股定理可得,AC=$\sqrt{B{C}^{2}-A{B}^{2}}$=2$\sqrt{3}$,
则$\overrightarrow{CA}$•$\overrightarrow{CB}$=|$\overrightarrow{CA}$|•|$\overrightarrow{CB}$|•cos∠ACB=2$\sqrt{3}$×4×$\frac{\sqrt{3}}{2}$=12.
故选A.
点评 本题考查向量的三角形法则和向量的数量积的定义的运用,同时考查三角形的外心的概念和勾股定理的运用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.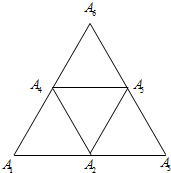 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )| A. | {-2,-1,0,1,2} | B. | $\left\{{-2,-1,-\frac{1}{2},0,\frac{1}{2},1,2}\right\}$ | ||
| C. | $\left\{{-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}}\right\}$ | D. | $\left\{{-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2},2}\right\}$ |
1.公差不为零的等差数列{an}的前n项和为Sn,若a3是a2与a6的等比中项,则$\frac{S_3}{a_3}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 1 | D. | 2 |
15.如图是一算法的程序框图,若此程序运行结果为s=55,则在判断框中应填入关于k的判断条件是( )


| A. | k≤11 | B. | k≤10 | C. | k≤9 | D. | k≤8 |
16.设数列{an}的前n项和为Sn,若a1=1,an+1=3Sn(n∈N*),则S6=( )
| A. | 44 | B. | 45 | C. | $\frac{1}{3}$(46-1) | D. | $\frac{{4}^{5}}{3}$ |
 如图,AB是⊙O的直径,C、F是⊙O上的点,AC是∠BAF的平分线,过点C作CD⊥AF,交AF的延长线于点D.
如图,AB是⊙O的直径,C、F是⊙O上的点,AC是∠BAF的平分线,过点C作CD⊥AF,交AF的延长线于点D.