Question

某工厂生产甲、乙两种产品，每种产品都是经过第一和第二工序加工而成，两道工序的加工结果相互独立，每道工序的加工结果均有A、B两个等级.对每种产品，两道工序的加工结果都为A级时，产品为一等品，其余均为二等品.

（1）已知甲、乙两种产品每一道工序的加工结果为A级的概率如表一所示，分别求生产出的甲、乙产品为一等品的概率P_甲、P_乙；

（2）已知一件产品的利润如表二所示，用ξ、η分别表示一件甲、乙产品的利润，在（1）的条件下，求ξ、η的分布列及Eξ、Eη；

（3）已知生产一件产品需用的工人数和资金额如表三所示.该工厂有工人40名，可用资金60万元.设x、y分别表示生产甲、乙产品的数量，在（2）的条件下，x、y为何值时，z=xEξ+yEη最大？最大值是多少？（解答时须给出图示）

表一

Answer 1

思路解析：本题主要综合考查了相互独立事件的概率、随机变量的分布列及期望、线性规划模型的建立与求解等知识.可以通过建立一个简单的数学模型来解决.

解：（1）P_甲=0.8×0.85=0.68,  P_乙=0.75×0.8=0.6.

（2）随机变量ξ、η的分别列是

ξ	5	2.5
P	0.68	0.32

 

η	2.5	1.5
P	0.6	0.4

Eξ=5×0.68+2.5×0.32=4.2,

Eη=2.5×0.6+1.5×0.4=2.1.

（3）由题设知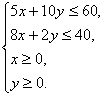

目标函数为z=xEξ+yEη=4.2x+2.1y.

作出可行域（如下图）：作直线l:4.2x+2.1y=0，得l向右上方平移l₁位置时，直线经过可行

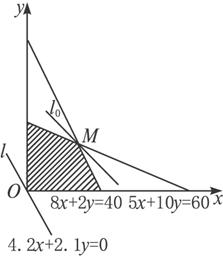
城上点M，点与原点距离最大，此时Z=4.2x+2.1y取最大值.

解方程组

得x=4,y=4.

即x=4,y=4时，z取最大值，z的最大值为25.2.