题目内容
袋子内有大小相同的15个小球,其中有n个红球,5个黄球,其余为白球.(1)从中任意摸出2球,求得到2球都是黄球的概率;
(2)如果从中任意摸出2球,得到都是红球或都是黄球的概率为
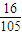 ,求红球个数;
,求红球个数;(3)根据(2)的结论,计算从袋中任意摸出3个小球得到至少有一个白球的概率.
【答案】分析:(1)由题意知本题是一个古典概型,试验包含的所有事件从15个球中摸出2球共有C152种结果,而满足条件的事件得到2球都是黄球有C52种结果,根据古典概型公式得到结果.
(2)由题意知本题是一个古典概型,试验发生包含的所有事件是从大小相同的15个小球中摸出2球共有C152种结果,而满足条件的事件是得到都是红球或都是黄球共有Cn2+C52种结果,根据古典概型公式得到结果.
(3)由题意知本题是一个古典概型,试验发生包含的所有事件是从大小相同的15个小球中摸出3球共有C153种结果,根据从袋中任意摸出3个小球得到至少有一个白球的对立事件的概率得到结果.
解答:解:(1)由题意知本题是一个古典概型,
试验包含的所有事件从15个球中摸出2球共有C152种结果,
而满足条件的事件得到2球都是黄球有C52种结果,
由古典概型公式得到P= =
= .
.
(2)设有n个红球,
由题意知本题是一个古典概型,
试验发生包含的所有事件是从大小相同的15个小球中摸出2球共有C152种结果,
而满足条件的事件是得到都是红球或都是黄球共有Cn2+C52种结果,
由题意知P= =
= ,
,
得到Cn2=6,
∴ ,
,
∴n=4,n=-3(舍去),
∴有4个红球.
(3)由(2)知有4个红球,故有6个白球.
设“摸出3个小球得到至少有1个白球”为事件A,
由题意知本题是一个古典概型,
试验发生包含的所有事件是从大小相同的15个小球中摸出3球共有C153种结果,
而满足条件的事件的对立事件是无白球,
则无白球的概率为P( )=
)= =
= =
= ,
,
∴至少有一个白球的概率为P(A)=1-P( )=1-
)=1- =
= ..
..
点评:本题主要考查古典概型和对立事件,正难则反是解题时要时刻注意的,我们尽量用简单的方法来解题,这样可以避免一些繁琐的运算,使得题目看起来更加清楚明了.
(2)由题意知本题是一个古典概型,试验发生包含的所有事件是从大小相同的15个小球中摸出2球共有C152种结果,而满足条件的事件是得到都是红球或都是黄球共有Cn2+C52种结果,根据古典概型公式得到结果.
(3)由题意知本题是一个古典概型,试验发生包含的所有事件是从大小相同的15个小球中摸出3球共有C153种结果,根据从袋中任意摸出3个小球得到至少有一个白球的对立事件的概率得到结果.
解答:解:(1)由题意知本题是一个古典概型,
试验包含的所有事件从15个球中摸出2球共有C152种结果,
而满足条件的事件得到2球都是黄球有C52种结果,
由古典概型公式得到P=
 =
= .
.(2)设有n个红球,
由题意知本题是一个古典概型,
试验发生包含的所有事件是从大小相同的15个小球中摸出2球共有C152种结果,
而满足条件的事件是得到都是红球或都是黄球共有Cn2+C52种结果,
由题意知P=
 =
= ,
,得到Cn2=6,
∴
 ,
,∴n=4,n=-3(舍去),
∴有4个红球.
(3)由(2)知有4个红球,故有6个白球.
设“摸出3个小球得到至少有1个白球”为事件A,
由题意知本题是一个古典概型,
试验发生包含的所有事件是从大小相同的15个小球中摸出3球共有C153种结果,
而满足条件的事件的对立事件是无白球,
则无白球的概率为P(
 )=
)= =
= =
= ,
,∴至少有一个白球的概率为P(A)=1-P(
 )=1-
)=1- =
= ..
..点评:本题主要考查古典概型和对立事件,正难则反是解题时要时刻注意的,我们尽量用简单的方法来解题,这样可以避免一些繁琐的运算,使得题目看起来更加清楚明了.

练习册系列答案
相关题目
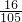 ,求红球个数;
,求红球个数;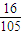 ,求红球个数;
,求红球个数;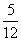 为
为