题目内容
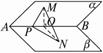
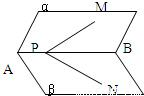
如图，P是二面角α—AB—β棱上的一点，分别在α、β平面上引射线PM、PN，如果∠BPM=∠BPN=45°，∠MPN=60°，那么二面角α—AB—β的大小为( )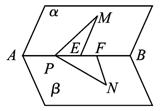
A.60° B.70° C.80° D.90°
解析：不妨设PM=a,PN=b,作ME⊥AB，NF⊥AB，则因∠EPM=∠FPM=45°，故PE=
,PF=
，于是
·
=(
-
)·(
-
)
=
·
-
·
-
·
+
·
=abcos60°-a·
cos45°+
·
-
·bcos45°=
=0.
因为EM、FN分别是α、β内的两条与棱AB垂直的直线，所以EM与FN之间的夹角就是欲求二面角的大小，所以α—AB—β的大小为90°.
答案：D
练习册系列答案
相关题目
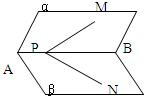如图，P是二面角α-AB-β棱AB上的一点，分别在α，β上引射线PM，PN，如果∠BPM=∠BPN=45°，∠MPN=60°，那么二面角α-AB-β的大小是
