题目内容
已知圆C的半径为1,圆心C在直线l1: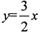 上,且其横坐标为整数,又圆C截直线
上,且其横坐标为整数,又圆C截直线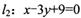 所得的弦长为
所得的弦长为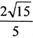 •
•
(I )求圆C的标准方程;
(II)设动点P在直线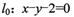 上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
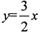 上,且其横坐标为整数,又圆C截直线
上,且其横坐标为整数,又圆C截直线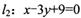 所得的弦长为
所得的弦长为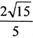 •
•(I )求圆C的标准方程;
(II)设动点P在直线
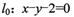 上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.
上,过点P作圆的两条切线PA, PB,切点分别为A ,B求四边形PACB面积的最小值.(Ⅰ)设圆心C的坐标为(2a,3a),a∈Z,则由题意可知:
 ,
,
解得:a=1.
∴所求圆C的标准方程为:(x-2)2+(y-3)2=1. ……………………………4分
(Ⅱ)因CA⊥PA,CB⊥PB,|PA|=|PB|,|AC|=1,
故S四边形PACB=2S△PAC=|AC| ·|PA|=|PA|=
·|PA|=|PA|= .
.
显然当PC⊥l0时,|PC|取得最小值,
∴ |PC|min= .
.
此时 .
.
即四边形PACB面积的最小值为 .
.
 ,
,解得:a=1.
∴所求圆C的标准方程为:(x-2)2+(y-3)2=1. ……………………………4分
(Ⅱ)因CA⊥PA,CB⊥PB,|PA|=|PB|,|AC|=1,
故S四边形PACB=2S△PAC=|AC|
 ·|PA|=|PA|=
·|PA|=|PA|= .
.显然当PC⊥l0时,|PC|取得最小值,
∴ |PC|min=
 .
.此时
 .
.即四边形PACB面积的最小值为
 .
.略

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
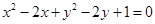 外一点
外一点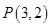 向这个圆作两条切线,则两切线夹角的正切值为( )
向这个圆作两条切线,则两切线夹角的正切值为( )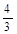
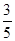
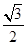
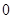
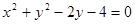 ,直线
,直线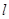 :mx-y+1-m=0
:mx-y+1-m=0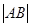 =3
=3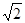 ,求直线
,求直线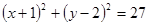 与
与 :
: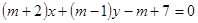 ,
,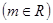
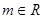 ,
, 此时
此时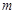 的值。
的值。 与圆
与圆 的交点,且经过点
的交点,且经过点 的圆的方程.
的圆的方程.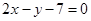 上的圆C与
上的圆C与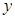 轴交于两点
轴交于两点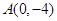 ,
,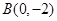 ,则圆C的方程为 .
,则圆C的方程为 .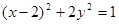 上,则
上,则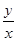 的最大值为( )
的最大值为( )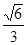
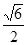
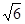
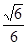
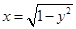 与直线
与直线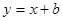 有两个交点,则
有两个交点,则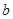 的取值范围是 .
的取值范围是 .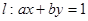 与圆
与圆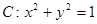 有两个不同的交点, 则点
有两个不同的交点, 则点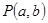 与圆
与圆 的位置关系是
的位置关系是