题目内容
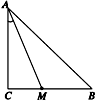
已知等腰Rt△ABC中，∠C=90°．在直角边BC上任取一点M，使∠CAM＜30°的概率为
．
| ||
| 3 |
| ||
| 3 |
分析：欲求∠CAM＜30°的概率，先求出M点可能在的位置的长度，及BC的长度，再让两者相除即可．
解答：解：在等腰直角三角形ABC中，设BC长为1，
在BC上取点D，使∠CAD=30°，则CD=
，
则若M点在线段CD上，满足条件．
∴使∠CAM＜30°的概率为
=
．
故答案为：
．
在BC上取点D，使∠CAD=30°，则CD=
| ||
| 3 |
则若M点在线段CD上，满足条件．
∴使∠CAM＜30°的概率为
| ||||
| 1 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查了概率里的古典概型．在利用几何概型的概率公式来求其概率时，几何“测度”可以是长度、面积、体积、角度等，其中对于几何度量为长度，面积、体积时的等可能性主要体现在点落在区域Ω上任置都是等可能的．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
=___________，
=__________．
=a,
=b,试用向量a、b表示
、
、
、
. 