Question

（2012•鹰潭模拟）如图，给定两个平面单位向量

OA

和

OB

，它们的夹角为120°，点C在以O为圆心的圆弧AB上，且

OC

=x

OA

+y

OB

（其中x，y∈R），则满足x+y≥

2

的概率为（　　）

• A．

  2

  -1
• B．

  3

  4

• C．

  π

  4

• D．

  π

  2

Answer 1

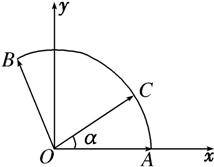
分析：根据题意，建立坐标系，设出A，B点的坐标，并设∠AOC=α，则由

OC

=x

OA

+y

OB

得x，y的值，从而求得x+y，结合正弦函数的性质可求满足条件的角α的范围，可求

解答：解：建立如图所示的坐标系，
则A（1，0），B（cos120°，sin120°），
即B（-

1

2

，

3

2

）
设∠AOC=α，则

OC

=（cosα，sinα）
∵

OC

=x

OA

+y

OB

=（x，0）+（-

1

2

y，

3

2

y）=（cosα，sinα）．
∴

x- 1 2 y=cosα 3 2 y=sinα

∴

y= 2sinα 3 x= sinα 3 +cosα

∴x+y=

3

sinα+cosα=2sin（α+30°）．
∵0°≤α≤120°．
∴30°≤α+30°≤150°．
当x+y≥

2

时，可得sin（α+30°）≥

2

2

∴45°≤α+30°≤135°即15°≤α≤105°，
∴满足x+y≥

2

的概率P=

105°-15°

120°

=

3

4

故选B

点评：本题是向量的坐标表示的应用，结合图形，利用三角函数的性质，容易求出结果．