题目内容
 如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部分,其体积分别记为
如图,在长方体ABCD-A1B1C1D1中,AB=6,AD=4,AA1=3,分别过BC、A1D1的两个平行截面将长方体分成三部分,其体积分别记为 ,
, .若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
.若V1:V2:V3=1:4:1,则截面A1EFD1的面积为
- A.
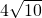
- B.

- C.
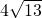
- D.16
C
分析:由题意先判断截面是一个矩形,由长方体的体积和各个几何体体积的比值,求出 的体积,根据柱体的体积公式求出AE,进而求出截面的另一边EA1长度,代入矩形面积公式求出截面的面积.
的体积,根据柱体的体积公式求出AE,进而求出截面的另一边EA1长度,代入矩形面积公式求出截面的面积.
解答:由题意知,截面是一个矩形,并且长方体的体积V=6×4×3=72,
∵V1:V2:V3=1:4:1,∴ =
= ×72=12,
×72=12,
则12= ×AE×A1A×AD,解得AE=2,
×AE×A1A×AD,解得AE=2,
在直角△AEA1中,EA1=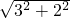 =
= ,
,
故截面的面积是EF×EA1=4 ,
,
故选C.
点评:本题主要考查了柱体的体积的求法,关键由题意和几何体的特征求出底面积和高,代入对应的体积公式进行求解.
分析:由题意先判断截面是一个矩形,由长方体的体积和各个几何体体积的比值,求出
 的体积,根据柱体的体积公式求出AE,进而求出截面的另一边EA1长度,代入矩形面积公式求出截面的面积.
的体积,根据柱体的体积公式求出AE,进而求出截面的另一边EA1长度,代入矩形面积公式求出截面的面积.解答:由题意知,截面是一个矩形,并且长方体的体积V=6×4×3=72,
∵V1:V2:V3=1:4:1,∴
 =
= ×72=12,
×72=12,则12=
 ×AE×A1A×AD,解得AE=2,
×AE×A1A×AD,解得AE=2,在直角△AEA1中,EA1=
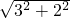 =
= ,
,故截面的面积是EF×EA1=4
 ,
,故选C.
点评:本题主要考查了柱体的体积的求法,关键由题意和几何体的特征求出底面积和高,代入对应的体积公式进行求解.

练习册系列答案
相关题目
 如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为:
如图在长方体ABCD-A1B1C1D1中,三棱锥A1-ABC的面是直角三角形的个数为: 如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )
如图,定义八个顶点都在某圆柱的底面圆周上的长方体叫做圆柱的内接长方体,圆柱也叫长方体的外接圆柱.设长方体ABCD-A1B1C1D1的长、宽、高分别为a,b,c(其中a>b>c),那么该长方体的外接圆柱侧面积的最大值等于( )

 .
. 
 ,AA1 =
,AA1 = ,M为侧棱CC1上一点,AM⊥BA1.
,M为侧棱CC1上一点,AM⊥BA1.