题目内容
已知函数f(x)=lnx-ax+1在x=2处的切线斜率为- .
.
(I)求实数a的值及函数f(x)的单调区间;
(II)设g(x)=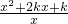 ,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
,对?x1∈(0,+∞),?x2∈(-∞,0)使得f(x1)≤g(x2)成立,求正实数k的取值范围;
(III)证明: +
+ +…+
+…+ <
<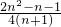 (n∈N*,n≥2)•
(n∈N*,n≥2)•
解:(Ⅰ)函数的定义域为(0,+∞).
由已知得:f′(x)= -a,f′(2)=
-a,f′(2)= -a=-
-a=- ,解得a=1.
,解得a=1.
于是f′(x)= -1=
-1=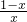 ,当x∈(0,1)时,f′(x)>0,f (x)为增函数,
,当x∈(0,1)时,f′(x)>0,f (x)为增函数,
当x∈(1,+∞)时,f′(x)<0,f (x)为减函数,
即f (x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(Ⅱ)由(Ⅰ)知,?x1∈(0,+∞),f (x1)≤f (1)=0,即f (x1)的最大值为0,
由题意知:对?x1∈(0,+∞),?x2∈(-∞,0)使得f (x1)≤g(x2)成立,
只须f (x)max≤g(x)max.
∵g(x)=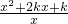 =x+
=x+ +2k=-(-x+
+2k=-(-x+ )+2k≤-2
)+2k≤-2 +2k,∴只须-2
+2k,∴只须-2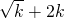 ≥0,解得k≥1.
≥0,解得k≥1.
故k的取值范围[1,+∞).
(Ⅲ)要证明: +
+ +…+
+…+ <
<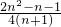 (n∈N*,n≥2)•
(n∈N*,n≥2)•
只须证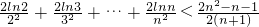 ,
,
即证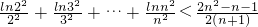 ,
,
由(Ⅰ)知,当x∈(1,+∞)时,f′(x)<0,f (x)为减函数,
∴f (x)=lnx-x+1≤f(1)=0,即lnx≤x-1,
∴当n≥2时,lnn2<n2-1,
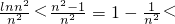 1-
1- =1-
=1-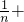
 ,
,
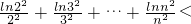 (1-
(1- +
+ )+(1-
)+(1- +
+ )+…+(1-
)+…+(1-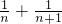 )
)
=n-1- +
+ =
=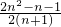 ,
,
∴ +
+ +…+
+…+ <
<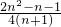 .
.
分析:(Ⅰ)由f′(2)=- 可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间.
可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间.
(Ⅱ)该问题可转化为解不等式f(x)max<g(x)max,进而转化为求函数的最值问题.
(Ⅲ)要证明 +
+ +…+
+…+ <
<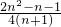 (n∈N*,n≥2),只须证
(n∈N*,n≥2),只须证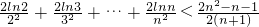 ,即证
,即证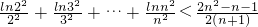 ,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.
,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.
点评:本题考查了导数的综合应用,用导数求单调区间、求最值、证明不等式,考查了分析问题解决问题的能力,本题运用了转化思想.
由已知得:f′(x)=
 -a,f′(2)=
-a,f′(2)= -a=-
-a=- ,解得a=1.
,解得a=1.于是f′(x)=
 -1=
-1=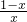 ,当x∈(0,1)时,f′(x)>0,f (x)为增函数,
,当x∈(0,1)时,f′(x)>0,f (x)为增函数,当x∈(1,+∞)时,f′(x)<0,f (x)为减函数,
即f (x)的单调递增区间为(0,1),单调递减区间为(1,+∞).
(Ⅱ)由(Ⅰ)知,?x1∈(0,+∞),f (x1)≤f (1)=0,即f (x1)的最大值为0,
由题意知:对?x1∈(0,+∞),?x2∈(-∞,0)使得f (x1)≤g(x2)成立,
只须f (x)max≤g(x)max.
∵g(x)=
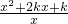 =x+
=x+ +2k=-(-x+
+2k=-(-x+ )+2k≤-2
)+2k≤-2 +2k,∴只须-2
+2k,∴只须-2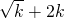 ≥0,解得k≥1.
≥0,解得k≥1.故k的取值范围[1,+∞).
(Ⅲ)要证明:
 +
+ +…+
+…+ <
<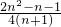 (n∈N*,n≥2)•
(n∈N*,n≥2)•只须证
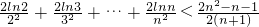 ,
,即证
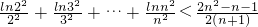 ,
,由(Ⅰ)知,当x∈(1,+∞)时,f′(x)<0,f (x)为减函数,
∴f (x)=lnx-x+1≤f(1)=0,即lnx≤x-1,
∴当n≥2时,lnn2<n2-1,
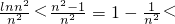 1-
1- =1-
=1-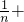
 ,
,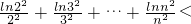 (1-
(1- +
+ )+(1-
)+(1- +
+ )+…+(1-
)+…+(1-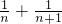 )
)=n-1-
 +
+ =
=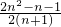 ,
,∴
 +
+ +…+
+…+ <
<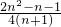 .
.分析:(Ⅰ)由f′(2)=-
 可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间.
可求得a值,在定义域内解不等式f′(x)>0,f′(x)<0可求单调区间.(Ⅱ)该问题可转化为解不等式f(x)max<g(x)max,进而转化为求函数的最值问题.
(Ⅲ)要证明
 +
+ +…+
+…+ <
<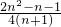 (n∈N*,n≥2),只须证
(n∈N*,n≥2),只须证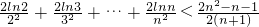 ,即证
,即证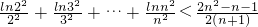 ,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.
,由f(x)的最大值得到一不等式,以此对该不等式左边各项进行放缩求和即可.点评:本题考查了导数的综合应用,用导数求单调区间、求最值、证明不等式,考查了分析问题解决问题的能力,本题运用了转化思想.

练习册系列答案
相关题目