题目内容
(2013•和平区二模)若关于x的不等式|x+2|+|x-3|≤|a-1|存在实数解,则实数a的取值范围是.
(-∞,-4]∪[6,+∞)
(-∞,-4]∪[6,+∞)
.分析:令f(x)=|x+2|+|x-3|,依题意,|a-1|≥f(x)存在实数解?|a-1|≥f(x)min=5,解此不等式即可.
解答:解:令f(x)=|x+2|+|x-3|,
则令f(x)=|x+2|+|x-3|≥|x+2+3-x|=5,
依题意,不等式|x+2|+|x-3|≤|a-1|存在实数解?|a-1|≥f(x)存在实数解?|a-1|≥f(x)min=5,
∴a-1≥5或a-1≤-5,
∴a≥6或a≤-4.
∴实数a的取值范围是(-∞,-4]∪[6,+∞).
故答案为:(-∞,-4]∪[6,+∞).
则令f(x)=|x+2|+|x-3|≥|x+2+3-x|=5,
依题意,不等式|x+2|+|x-3|≤|a-1|存在实数解?|a-1|≥f(x)存在实数解?|a-1|≥f(x)min=5,
∴a-1≥5或a-1≤-5,
∴a≥6或a≤-4.
∴实数a的取值范围是(-∞,-4]∪[6,+∞).
故答案为:(-∞,-4]∪[6,+∞).
点评:本题考查绝对值不等式,考查构造函数思想与等价转化思想的综合应用,考查函数的最值与解不等式的能力,属于中档题.

练习册系列答案
相关题目
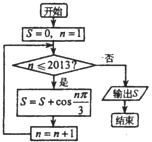 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )