题目内容
已知函数
，
（I）求f（-
），
），
）的值；
（Ⅱ）做出函数的简图；
（III）求函数的最大值和最小值．
解：（Ⅰ）当-1≤x≤0时，f（x）=-x
∴f（-）=-（-）=
当0≤x＜1时，f（x）=x2
∴f（
）=（）2=
当1≤x≤2时，f（x）=x
∴f（
）=
（Ⅱ）如右图
（Ⅲ）根据函数图象可知f（x）max=f（2）=2；
f（x）min=f（0）=0
分析：（I）根据-、、分别属于哪段区间就分别代入所对应的表达式，解之即可求出所求；
（II）根据分段函数图象的特点可知画图是进行分段画即可；
（III）观察图象即可求出函数的最大值和最小值．
点评：本题主要考查了求函数值以及画图和求函数的最值，同时考查了数形结合的数学思想，属于基础题．
∴f（-
）=-（-）=当0≤x＜1时，f（x）=x2
∴f（
）=（）2=当1≤x≤2时，f（x）=x
∴f（
）=（Ⅱ）如右图
（Ⅲ）根据函数图象可知f（x）max=f（2）=2；
f（x）min=f（0）=0
分析：（I）根据-
、、分别属于哪段区间就分别代入所对应的表达式，解之即可求出所求；（II）根据分段函数图象的特点可知画图是进行分段画即可；
（III）观察图象即可求出函数的最大值和最小值．
点评：本题主要考查了求函数值以及画图和求函数的最值，同时考查了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
．
．
．
=（
，0）平移得到函数g（x）的图象，求函数g（x）在区间[0，π]上的最大值和最小值．
．
成等差数列，且
=9，求a的值．
．
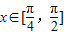时，不等式|f（x）-m|＜2恒成立，求实数m的取值范围．