题目内容
函数y=f(x)的图象与y=2x的图象关于直线y=x对称,则函数y=f(4x-x2)的递增区间是 .
∵y=2x的反函数为y=log2x,
∴f(x)=log2x,f(4x-x2)=log2(4x-x2).
令t=4x-x2,则t>0,即4x-x2>0,∴x∈(0,4),
又∵t=-x2+4x的对称轴为x=2,且对数的底数大于1,∴y=f(4x-x2)的递增区间为(0,2).
答案:(0,2)

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
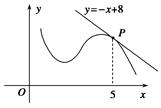


 sinx在[0,π]上的大致图象是( )
sinx在[0,π]上的大致图象是( )


 x+2,则f(1)+f′(1)=_____.
x+2,则f(1)+f′(1)=_____.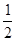 x2+
x2+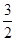 x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.
x,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图象上.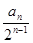 ,求数列{bn}的前n项和Tn
,求数列{bn}的前n项和Tn