题目内容
设函数f(x)=x3-x2-x+2.(Ⅰ)求f(x)的单调区间和极值;
(Ⅱ)若当x∈[-1,2]时,-3≤af(x)+b≤3,求a-b的最大值.
【答案】分析:(1)先对函数f(x)进行求导,令f'(x)>0解出x的范围得到其增区间,同理令f'(x)<0解出x的范围得到减区间;令f'(x)=0解出x的值得到极值点.
(2)先求出函数f(x)在区间[-1,2]上的最大与最小值,由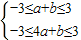 可得答案.
可得答案.
解答:解:(Ⅰ)f'(x)=3x2-2x-1=(3x+1)(x-1).
于是,当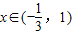 时,f'(x)<0;
时,f'(x)<0;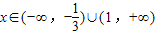 时,f'(x)>0.
时,f'(x)>0.
故f(x)在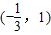 单调减少,在
单调减少,在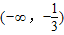 ,(1,+∞)单调增加.
,(1,+∞)单调增加.
当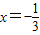 时,f(x)取得极大值
时,f(x)取得极大值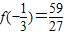 ;
;
当x=1时,f(x)取得极小值f(1)=1.
(Ⅱ)根据(Ⅰ)及f(-1)=1,f(2)=4,f(x)在[-1,2]的最大值为4,最小值为1.
因此,当x∈[-1,2]时,-3≤af(x)+b≤3的充要条件是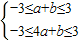 ,
,
即a,b满足约束条件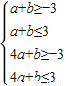 ,
,
由线性规划得,a-b的最大值为7.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系和函数的极值点与导数的关系,即令导数大于0可求函数的增区间,令导数小于0可求函数的减区间,令导数等于0可求其极值点.
(2)先求出函数f(x)在区间[-1,2]上的最大与最小值,由
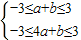 可得答案.
可得答案.解答:解:(Ⅰ)f'(x)=3x2-2x-1=(3x+1)(x-1).
于是,当
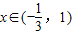 时,f'(x)<0;
时,f'(x)<0;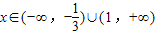 时,f'(x)>0.
时,f'(x)>0.故f(x)在
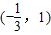 单调减少,在
单调减少,在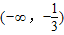 ,(1,+∞)单调增加.
,(1,+∞)单调增加.当
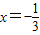 时,f(x)取得极大值
时,f(x)取得极大值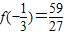 ;
;当x=1时,f(x)取得极小值f(1)=1.
(Ⅱ)根据(Ⅰ)及f(-1)=1,f(2)=4,f(x)在[-1,2]的最大值为4,最小值为1.
因此,当x∈[-1,2]时,-3≤af(x)+b≤3的充要条件是
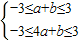 ,
,即a,b满足约束条件
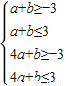 ,
,由线性规划得,a-b的最大值为7.
点评:本题主要考查函数的单调性与其导函数的正负之间的关系和函数的极值点与导数的关系,即令导数大于0可求函数的增区间,令导数小于0可求函数的减区间,令导数等于0可求其极值点.

练习册系列答案
相关题目