题目内容
已知函数f（x）是定义域为（-∞，0）∪（0，+∞）的奇函数，在区间（0，+∞）上单调递增，且f（-2）=0．若
＜0，则x的取值范围是 ．
| f(2x+1) | 4x-1 |
分析：由函数的奇偶性、单调性及特殊点可作出函数的草图，根据图象可把不等式转化为具体不等式组，解出即可．
解答：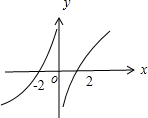
解：∵f（x）是定义域为（-∞，0）∪（0，+∞）的奇函数，在区间（0，+∞）上单调递增，
∴f（x）在区间（-∞，0）上也单调递增，
∵f（-2）=0，∴f（2）=-f（-2）=0，
作出函数f（x）的草图如图所示：
由图象可得，
＜0?
或
?
或
，
解得-
＜x＜-
，或
＜x＜
，
所以x的取值范围为：-
＜x＜-
，或
＜x＜
，
故答案为：-
＜x＜-
，或
＜x＜
．
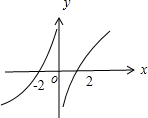解：∵f（x）是定义域为（-∞，0）∪（0，+∞）的奇函数，在区间（0，+∞）上单调递增，∴f（x）在区间（-∞，0）上也单调递增，
∵f（-2）=0，∴f（2）=-f（-2）=0，
作出函数f（x）的草图如图所示：
由图象可得，
| f(2x+1) |
| 4x-1 |
|
|
|
|
解得-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
所以x的取值范围为：-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
故答案为：-
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
点评：本题考查函数的单调性、奇偶性及其应用，考查抽象不等式的求解，考查数形结合思想，利用图象使问题变得直观明了．
练习册系列答案
相关题目
已知函数f（x）=x+