Question

【题目】设双曲线 的两个焦点分别为F1、F2离心率e=2.
（1）求此双曲线的渐近线l1、l2的方程；
（2）若A、B分别为l1、l2上的点，且 求线段AB的中点M的轨迹方程.
（3）过点N（1，0）能否作直线l ， 使l与双曲线交于不同两点P、Q.且 ，若存在，求直线l的方程，若不存在，说明理由.

Answer 1

【答案】
（1）

【解答】双曲线离心率为, ，所以渐近线方程：

（2）

【解答】设A（x1，y1）、B（x2，y2）AB的中点M（x，y）∵2|AB|=5|F1F2|∴|AB|=10

∴(x1，x2)2+(y1–y2)2=100，又 ， ，x1+x2=2x，y1+y2=2y．

∴ ，

∴ , 即

（3）

【解答】假设存在这样的直线e，设其方程为y=k(x-1) P(x1，y1)，Q(x2，y2)∵

∴x1x2+y1y2=0 ∴x1x2+k2[x1x2-(x1+x2)+1]=0 ①

由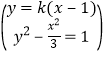 得(3k2-1)x2-6k2x+3k2-3=0 ∴ 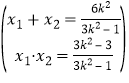②

由①②得： k2+3=0 ∴k不存在，即这样的直线不存在．

【解析】本题考查了双曲线的定义分析问题、解决问题的能力