Question

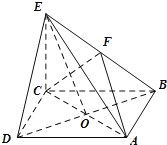
【题目】如图，△ABC是边长为4的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，且EC⊥平面ABC，EC=2．
（1）证明：DE∥平面ABC；
（2）证明：AD⊥BE．

Answer 1

【答案】证明：（1）取AB的中点F，连接DF，CF，
∵△ABC是边长为4的等边三角形，△ABD是等腰直角三角形，AD⊥BD，平面ABC⊥平面ABD，
∴DF⊥CF，
∵DF=BC=2
又∵EC⊥平面ABC，既有：EC⊥FC，EC=2．
∴DFEC，故四边形DEFC为平行四边形，
∴DE∥FC
∴DE平面ABC，可得DE∥平面ABC．
（2）以FA，FC，FD为x，y，z轴的正方向建立直角坐标系，
则有：A（2，0，0），D（0，0，2），B（﹣2，0，0），E（0，2，2）
=（﹣2，0，2），=（﹣2，2，2）
由于=0，
故AD⊥BE．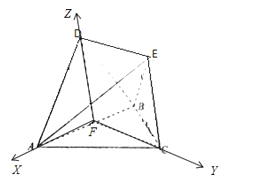

【解析】（1）取AB的中点F，连接DF，CF，由已知可证DFEC，可得四边形DEFC为平行四边形，可得DE∥FC，由DE平面ABC，从而可证DE∥平面ABC．
（2）以FA，FC，FD为x，y，z轴的正方向建立直角坐标系，求出向量 ， 的坐标，由=0，即可证明AD⊥BE．