题目内容
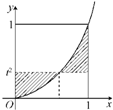 由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是多少?
由曲线y=x2和直线y=t2(0<t<1),x=1,x=0所围成的图形(阴影部分)的面积的最小值是多少?分析:根据定积分的几何意义,阴影部分的面积为y=t2-x2在[0,t]上的积分值,加上y=x2-t2在[t,1]上的积分值所得的和.由积分计算公式,算出S(t)=
t3-t2+
,再通过求导讨论S(t)的单调性,得当t=
时,S(t)有最小值为
,即得阴影部分面积的最小值.
| 4 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
解答:解:根据定积分的几何意义,阴影部分的面积为
S(t)=
(t2-x2)dx+
(x2-t2)dx
=(t2x-
x3)
+(
x3-t2x)
=
t3-t2+
求导数,得S'(t)=4t2-2t=4t(t-
)
令S'(t)=0得t=
或t=0…(6分)
∵0<t<
时,S'(t)<0;
<t<1时,S'(t)>0
∴函数S(t)在(0,
)上是减函数;在(
,1)上是增函数
因此,当t=
时,函数S(t)取极小值,并且这个极小值也是函数的最小值.
∴阴影部分的面积S(t)的最小值是S(
)=
.
S(t)=
| ∫ | t 0 |
| ∫ | 1 t |
=(t2x-
| 1 |
| 3 |
| | | t 0 |
| 1 |
| 3 |
| | | 1 t |
=
| 4 |
| 3 |
| 1 |
| 3 |
求导数,得S'(t)=4t2-2t=4t(t-
| 1 |
| 2 |
令S'(t)=0得t=
| 1 |
| 2 |
∵0<t<
| 1 |
| 2 |
| 1 |
| 2 |
∴函数S(t)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
因此,当t=
| 1 |
| 2 |
∴阴影部分的面积S(t)的最小值是S(
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题给出曲线围成的图形,求图形面积的最小值,着重考查了定积分的几何意义和利用导数研究函数的单调性与最值等知识,属于中档题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
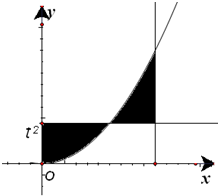 由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
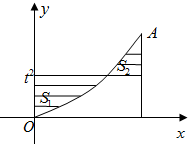 由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )
由曲线y=x2和直线x=0,x=1,y=t2,t∈(0,1)所围成的图形(阴影部分)的面积的最小值为( )