Question

a＞0，且a≠1，函数f（x）log_a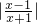在（1，+∞）单调递减，则f（x）

1. A.
   在（-∞，-1）上单调递减，在（-1，1）上单调递增
2. B.
   在（-∞，-1）上单调递增，在（-1，1）上单调递减
3. C.
   在（-∞，-1）上单调递增，在（-1，1）上单调递增
4. D.
   在（-∞，-1）上单调递减，在（-1，1）上单调递减

Answer 1

A
分析：先判断当x＞1时t=||的单调性，由f（x）在（1，+∞）上单调性可知y=log_ax单调性，根据t=||在（-∞，-1），（-1，1）上的单调性及y=log_ax的单调性即可判断f（x）的单调性．
解答：当x＞1时，t=||==1-，单调递增，
而f（x）在（1，+∞）上单调递减，
所以y=log_ax单调递减，即0＜a＜1，
当x＜-1时，t=||==1-，单调递增，
又y=log_ax单调递减，
所以f（x）在（-∞，-1）上单调递减，
当-1＜x＜1时，t=||=-=-1+，单调递减，
又y=log_ax单调递减，
所以f（x）在（-1，1）上单调递增，
故选A．
点评：本题考查对数函数、复合函数的单调性的判定，复合函数单调性的判断方法为：“同增异减”，要准确理解．