题目内容
已知-1≤x≤1,n≥2,求证:(1-x)n+(1+x)n≤2n.
证明:∵-1≤x≤1,设x=cos2θ.
则1-x=1-cos2θ=1-(1-2sin2θ)=2sin2θ,1+x=2cos2θ.
∴(1-x)n+(1+x)n=(2sin2θ)n+(2cos2θ)n
=2n(sin2nθ+cos2nθ).
考虑指数函数y=ax,
当a∈(0,1)时,在x∈(0,+∞)上单调递减,
∴sin2nθ≤sin2θ,
cos2nθ≤cos2θ.
∴2n(sin2nθ+cos2nθ)≤2n(sin2θ+cos2θ)=2n.
∴(1-x)n+(1+x)n≤2n.

练习册系列答案
相关题目
 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点. <t<2,bn=
<t<2,bn=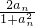 (n∈N*),求证:
(n∈N*),求证: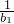 +
+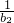 +…+
+…+ <2n-
<2n- .
. 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点. <t<2,bn=
<t<2,bn= (n∈N*),求证:
(n∈N*),求证: +
+ +…+
+…+ <2n-
<2n- .
.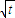 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点. <t<2,bn=
<t<2,bn=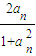 (n∈N*),求证:
(n∈N*),求证: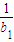 +
+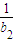 +…+
+…+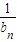 <2n-
<2n-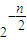 .
. 是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点.
是函数f(x)=an-1x3-3[(t+1)an-an+1]x+1(n≥2)的一个极值点. <t<2,bn=
<t<2,bn= (n∈N*),求证:
(n∈N*),求证: +
+ +…+
+…+ <2n-
<2n- .
.