题目内容
 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中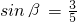 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
(1)求S关于p的函数关系;
(2)当p为何值时,抢救最及时?
 解:(1)建立如图所示的直角坐标系,
解:(1)建立如图所示的直角坐标系,∵
 ,∴
,∴ ,
, ,∴N点的坐标为(3a,4a).
,∴N点的坐标为(3a,4a).又射线OA的方程为y=3x,
又B(p,0),∴直线BN的方程为

∴
 .…
.…当p=3a时,C(3a,9a),
 .
.当p≠3a时,方程组
 ,解为
,解为
∴点C的坐标为
 .
.∴
 .对p=3a也成立.
.对p=3a也成立.∴
 .…
.…(2)由(1)得
 .
.令
 ,∴
,∴ ,
,当且仅当
 ,即
,即 ,此时
,此时 ,上式取等号,∴当
,上式取等号,∴当 Km时,S有最小值,即抢救最及时.…
Km时,S有最小值,即抢救最及时.…分析:(1)由已知中射线OA行驶(北偏东α角),其中
 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中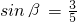 .我们可能建立直角坐标系,分别求出直线的方程和点的坐标,进而可以得到S关于p的函数关系;
.我们可能建立直角坐标系,分别求出直线的方程和点的坐标,进而可以得到S关于p的函数关系;(2)p为何值时,抢救最及时,可转化为求函数的最小值,根据(1)中的函数解析式,利用基本不等式,可求出函数的最小值,进而得到答案.
点评:本题考查的知识点是函数模型的选择与应用,其中解答的关键是建立平面直角坐标系,将题目中的相关直线、点的方程或坐标具体化,进而拟合出函数模型.

练习册系列答案
 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
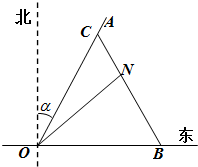 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.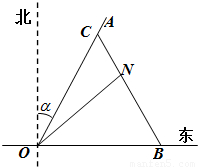 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中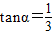 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中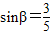 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.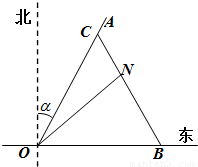 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中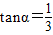 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中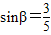 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.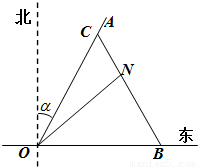 如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中
如图所示,一辆载着重危病人的火车从O地出发,沿射线OA行驶(北偏东α角),其中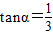 ,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中
,在距离O地5a km(a为正数)北偏东β角的N处住有一位医学专家,其中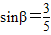 .现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.
.现110指挥部紧急征调离O地正东p km的B处的救护车赶往N处载上医学专家全速追赶载有重危病人的火车,并在C处相遇,经测算当辆车行驶路线与OB围成的三角形OBC面积S最小时,抢救最及时.