Question

【题目】已知函数f（x）= ，直线y= x（a≠0）为曲线y=f（x）的一条切线．
（1）求实数a的值；
（2）用min{m，n}表示m，n中的最小值，设函数g（x）=min{f（x），x﹣ }（x＞0），若函数h（x）=g（x）﹣bx2为增函数，求实数b的取值范围．

Answer 1

【答案】
（1）解：设切点坐标为（x0，y0），f′（x）= ，则 ，∴a=1；
（2）解：记F（x）=f（x）﹣（x﹣ ），x＞0．下面考察y=F（x）的符号．

求导F′（x）= ﹣1﹣ ，

x≥2，F′（x）＜0，0＜x＜2，x（2﹣x）≤1，∴F′（x）= ﹣1﹣ ≤﹣ ＜0，

∴F（x）在（0，+∞）上单调递减，

∵F（1）= ＞0，F（2）= ﹣ ＜0，

∴F（x）在[1，2]上有唯一零点x0，

∴g（x）= ，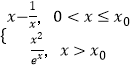

∴h（x）=g（x）﹣bx2= ，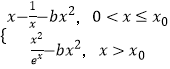

x＞x0，h′（x）= ﹣2bx≥0恒成立，∴2b≤ ，

设u（x）= ，u′（x）= ，函数在（x0，3）上单调递减，（3，+∞）上单调递增，

∴u（x）min=﹣ ，∴2b≤﹣ ，∴b≤﹣ ；

0＜x≤x0时，h′（x）=1+ ﹣2bx，b≤0，h′（x）＞0在（0，x0）上恒成立，

综上所述，b≤﹣ 时，函数h（x）=g（x）﹣bx2为增函数．

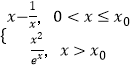【解析】（1）根据直线y= x（a≠0）为曲线y=f（x）的一条切线，求实数a的值；（2）记F（x）=f（x）﹣（x﹣ ），x＞0．考察y=F（x）的符号，得出g（x）= ，再分类讨论，利用导数的正负，即可得出结论．
【考点精析】掌握利用导数研究函数的单调性是解答本题的根本，需要知道一般的,函数的单调性与其导数的正负有如下关系： 在某个区间内，(1)如果，那么函数在这个区间单调递增；(2)如果，那么函数在这个区间单调递减．