题目内容
16.已知函数数列{an},a1=1,${a}_{n-1}=\frac{5{a}_{n}}{{a}_{n}+5}$,则数列{an}的通项an=$\frac{5}{6-n}$.分析 根据数列的递推关系,利用取倒数法进行求解即可.
解答 解:∵a1=1,${a}_{n-1}=\frac{5{a}_{n}}{{a}_{n}+5}$,
∴取倒数得$\frac{1}{{a}_{n-1}}$=$\frac{{a}_{n}+5}{5{a}_{n}}$=$\frac{1}{5}$+$\frac{1}{{a}_{n}}$,
即$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=-$\frac{1}{5}$,
即数列{$\frac{1}{{a}_{n}}$}是以公差d=-$\frac{1}{5}$,首项为$\frac{1}{{a}_{1}}=1$的等差数列,
则$\frac{1}{{a}_{n}}$=1-$\frac{1}{5}$(n-1)=$\frac{6-n}{5}$,
∴数列{an}的通项an=$\frac{5}{6-n}$,
故答案为:$\frac{5}{6-n}$.
点评 本题主要考查数列通项公式的求解,利用数列的递推关系,利用取倒数法是解决本题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
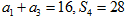
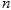 取何值时Sn最大,并求出这个最大值
取何值时Sn最大,并求出这个最大值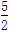 )等于( )
)等于( )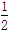 B.-
B.-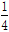 C.
C.