题目内容
已知函数f(x)=axlnx(a≠0).
(Ⅰ)求函数f(x)的单调区间和最值;
(Ⅱ)若m>0,n>0,a>0,证明:f(m)+f(n)≥f(m+n)-a(m+n)ln2.
(Ⅰ)∵f'(x)=alnx+a(x>0),
当a>0时,令f'(x)≥0,即lnx≥-1=lne-1.
∴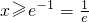 .,∴
.,∴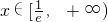 .
.
同理,令f'(x)≤0,可得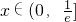 .
.
∴f(x)单调递增区间为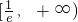 ,单调递减区间为
,单调递减区间为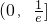 .
.
由此可知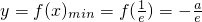 .无最大值.
.无最大值.
当a<0时,令f'(x)≥0,即lnx≤-1=lne-1.∴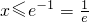 .,∴
.,∴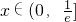 .
.
同理,令f'(x)≤0可得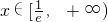 .
.
∴f(x)单调递增区间为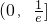 ,单调递减区间为
,单调递减区间为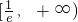 .
.
由此可知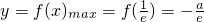 .此时无最小值.
.此时无最小值.
(Ⅱ)不妨设m≥n>0,令n=x,
记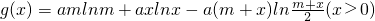

∵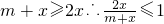 ,∴
,∴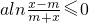 ,
,
∴g'(x)≤0,∴g(x)是减函数,
∵m≥x>0,∴g(x)≥g(m)=0∴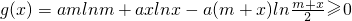 ,即得证.
,即得证.
分析:(Ⅰ)f'(x)=alnx+a(x>0),当a>0时f(x)单调递增区间为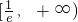 ,单调递减区间为
,单调递减区间为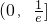 .当a<0时f(x)单调递增区间为
.当a<0时f(x)单调递增区间为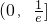 ,单调递减区间为
,单调递减区间为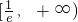 .
.
(Ⅱ)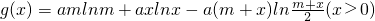 可得
可得 可以证得g'(x)≤0,∴g(x)是减函数,
可以证得g'(x)≤0,∴g(x)是减函数,
∴g(x)≥g(m)=0
点评:解决此类问题的关键是先求函数的导数讨论其中的参数得到函数的单调性进而得到函数的最值,证明不等式一般是抽象出一个新的函数利用导函数的单调性进行证明,研究函数的单调性、最值、证明不等式是解答题考查的一个重点.
当a>0时,令f'(x)≥0,即lnx≥-1=lne-1.
∴
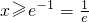 .,∴
.,∴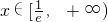 .
.同理,令f'(x)≤0,可得
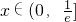 .
.∴f(x)单调递增区间为
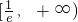 ,单调递减区间为
,单调递减区间为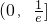 .
.由此可知
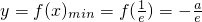 .无最大值.
.无最大值.当a<0时,令f'(x)≥0,即lnx≤-1=lne-1.∴
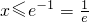 .,∴
.,∴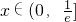 .
.同理,令f'(x)≤0可得
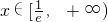 .
.∴f(x)单调递增区间为
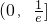 ,单调递减区间为
,单调递减区间为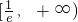 .
.由此可知
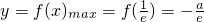 .此时无最小值.
.此时无最小值.(Ⅱ)不妨设m≥n>0,令n=x,
记
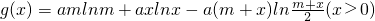

∵
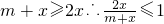 ,∴
,∴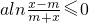 ,
,∴g'(x)≤0,∴g(x)是减函数,
∵m≥x>0,∴g(x)≥g(m)=0∴
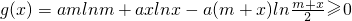 ,即得证.
,即得证.分析:(Ⅰ)f'(x)=alnx+a(x>0),当a>0时f(x)单调递增区间为
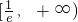 ,单调递减区间为
,单调递减区间为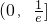 .当a<0时f(x)单调递增区间为
.当a<0时f(x)单调递增区间为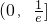 ,单调递减区间为
,单调递减区间为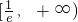 .
.(Ⅱ)
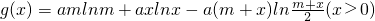 可得
可得 可以证得g'(x)≤0,∴g(x)是减函数,
可以证得g'(x)≤0,∴g(x)是减函数,∴g(x)≥g(m)=0
点评:解决此类问题的关键是先求函数的导数讨论其中的参数得到函数的单调性进而得到函数的最值,证明不等式一般是抽象出一个新的函数利用导函数的单调性进行证明,研究函数的单调性、最值、证明不等式是解答题考查的一个重点.

练习册系列答案
相关题目