��Ŀ����
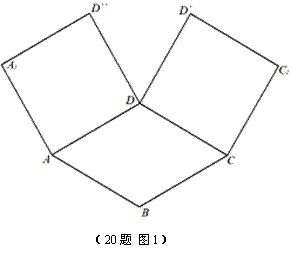
����С������12�֣���ͼ1����ƽ���ڣ�ABCD�߳�Ϊ2�������Σ�![]() ��
��![]() ��
��
�������Ρ������������ηֱ���AD��CD����ʹ![]() ��
��![]() �غ��ڵ�D1����ֱ��l����B
�غ��ڵ�D1����ֱ��l����B
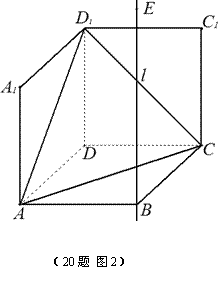
�Ҵ�ֱ��������ABCD���ڵ�ƽ�棬��E��ֱ��l�ϵ�һ�����㣬�����D1λ��ƽ��ABCD
ͬ�࣬��![]() ��ͼ2����
��ͼ2����
��1��������E �C AC �C D1�Ĵ�СΪq ����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
 ��2����
��2����![]() ʱ���߶�
ʱ���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ��ʹƽ��
��ʹƽ��![]() ƽ��
ƽ��![]() �������ڣ����
�������ڣ����![]() ��
��![]() ���ɵı�
���ɵı�![]() ���������ڣ���˵�����ɡ�
���������ڣ���˵�����ɡ�
 |
�⣺��1������DB��AC�ڵ�O������DO��EO����![]() �У�
�У�![]() AD=DC
AD=DC
![]()
![]() ��ͬ����֤��
��ͬ����֤��![]()
![]()
![]() Ϊ�������ǵ�ƽ���
Ϊ�������ǵ�ƽ���![]() ��������3��
��������3��
��![]() ��
��![]() ��
��
ͬ���ɵã�![]() ��
��![]() .
.
������![]() �У������Ҷ����õ��� cos
�У������Ҷ����õ��� cos![]() =
=![]() �� ��������6��
�� ��������6��
ע�����귨�������֡�
��2������DΪԭ�㣬��DA��DC,DD1����ֱ�߷ֱ�Ϊx,y,z�ᣬ�����ռ�ֱ������ϵ��ͼ��ʾ��BE = t (t>2).
![]() ��E(2,2,t) ��7��
��E(2,2,t) ��7��


![]()
![]() ������9��
������9��
��ƽ��![]() �ķ�����
�ķ�����![]()
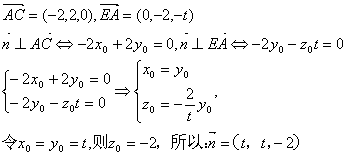 ����������������10��
����������������10��
��ƽ��![]() ƽ��
ƽ��![]() ����
����![]() ƽ��
ƽ��![]() ��
��
![]() ����������������11��
����������������11��
���ԣ����߶�![]() ���Ǵ��ڵ�
���Ǵ��ڵ�![]() ��ʹƽ��
��ʹƽ��![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ���ɵı�
���ɵı�![]() ��������12��
��������12��
ע�����η���������

 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�