题目内容
已知y=f（x）在定义域（-3，6）内可导，其图象如图，其导函数为y=f′（x），则不等式f′（x）≤0的解集为
[-1，2]∪[4，6）
[-1，2]∪[4，6）
分析：欲求不等式f′（x）≤0的解集即求函数f（x）的单调减区间，然后结合图象即可得到结论．
解答：解：不等式f′（x）≤0的解集即为f（x）的单调减区间
根据f（x）的图象可知f（x）的单调减区间为[-1，2]，[4，6）
故答案为：[-1，2]∪[4，6）
根据f（x）的图象可知f（x）的单调减区间为[-1，2]，[4，6）
故答案为：[-1，2]∪[4，6）
点评：本题主要考查了函数的单调性与导数的关系，同时考查了识图能力，属于基础题．
练习册系列答案
相关题目
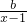-a（a∈R，a≠0）在x=3处的切线方程为（2a-1）x-2y+3=0
-a（a∈R，a≠0）在x=3处的切线方程为（2a-1）x-2y+3=0
-a（a∈R，a≠0）在x=3处的切线方程为（2a-1）x-2y+3=0