题目内容
设![]() 是定义在R上的奇函数,
是定义在R上的奇函数,![]() 与
与![]() 的图象关于直线x = 1对称,当
的图象关于直线x = 1对称,当![]() 时,
时,![]() 。
。
(1)求![]() 的解析式;
的解析式;
(2)当x = 1时,![]() 取得极值,证明:对任意x1、
取得极值,证明:对任意x1、![]() ,不等式
,不等式
![]() 。
。
(3)若![]() 是
是![]() 上的单调函数,且当
上的单调函数,且当![]() 时有
时有![]() ,
,
证明:![]() 。
。
解:①∵![]() 与
与![]() 的图象关于直线x = 1对称当
的图象关于直线x = 1对称当![]() 时,设
时,设![]() 为
为![]() 上的点
上的点
∴P关于x = 1对称点![]()
则![]()
∴![]()
∴![]()
又∵![]() 在R上是奇函数, ∴
在R上是奇函数, ∴![]()
又设![]() ∴
∴![]()
∴![]()
∴![]()
∴![]() ∴
∴![]()
②![]()
∴![]() ∴
∴![]() ∴
∴![]()
∴![]()
∵![]() 有
有![]() ∴
∴![]()
∴![]() 即
即![]() 在(-1,1)上为单调减函数,在
在(-1,1)上为单调减函数,在![]() 上有
上有
![]()
![]()
则![]() 上恒有:
上恒有:![]()
③若![]() 在
在![]() 单调递减,则
单调递减,则![]()
∴![]()
![]() 上不恒成。
上不恒成。
故a不存在,∴![]() 在
在![]() 递增
递增
∴![]() 在
在![]() 上恒成立。∴
上恒成立。∴![]()
不妨假设![]() ,则
,则![]()
已知![]() 矛盾
矛盾
若![]() 则
则![]() 与
与![]() (矛盾)
(矛盾)
∴综上可知![]()

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
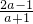 ,则a的取值范围是________.
,则a的取值范围是________. ,则a的取值范围是 .
,则a的取值范围是 .