题目内容
(理)二项式(x3+
)n的展开式中,只有第6项的系数最大,则该展开式中的常数项为
(文)已知x>0,y>0,x+y=1,求lgx+lgy的最大值是
| 1 | x2 |
210
210
;(文)已知x>0,y>0,x+y=1,求lgx+lgy的最大值是
-2lg2
-2lg2
.分析:(1)根据展开式中,只有第6项的系数最大,可求n=10,写出其通项公式,令x的指数为0,即可求出展开式中的常数项;(2)由已知条件,可根据以得到 xy≤(
)2=
,从而得出lg(xy)的最大值
| x+y |
| 2 |
| 1 |
| 4 |
解答:解:(1)由题意,n=10,Tr+1=
×(x3) 10-r×(
)r=
x 30-5r
令30-5r=0,∴r=6
∴展开式中的常数项为T7=C106=210
(2)∵x>0,y>0,x+y=1∴xy≤(
)2=
又 lgx+lgy=lg(xy)≤lg(
)2=lg
=-2lg2,
故答案为:210;-2lg2.
| C | r 10 |
| 1 |
| x2 |
| C | r 10 |
令30-5r=0,∴r=6
∴展开式中的常数项为T7=C106=210
(2)∵x>0,y>0,x+y=1∴xy≤(
| x+y |
| 2 |
| 1 |
| 4 |
又 lgx+lgy=lg(xy)≤lg(
| x+y |
| 2 |
| 1 |
| 4 |
故答案为:210;-2lg2.
点评:本题主要考查二项式定理的运用,考查基本不等式,解题的关键是写出展开式的通项,对对数式合理变形.

练习册系列答案
相关题目
 )n的展开式中,只有第6项的系数最大,则该展开式中的常数项为________;
)n的展开式中,只有第6项的系数最大,则该展开式中的常数项为________;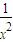 )n的展开式中,只有第6项的系数最大,则该展开式中的常数项为 ;
)n的展开式中,只有第6项的系数最大,则该展开式中的常数项为 ;