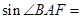题目内容
如图所示,在正方体ABCD A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是 .
A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是 .

 A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是 .
A1B1C1D1中,M、N分别是棱CD、CC1的中点,则异面直线A1M与DN所成的角的大小是 . 
90°
如图所示,取CN的中点K,连接MK,则MK为△CDN的中位线,所以MK∥DN.

所以∠A1MK为异面直线A1M与DN所成的角.连接A1C1,AM.设正方体棱长为4,
则A1K= =
= ,
,
MK= DN=
DN= =
= ,
,
A1M= =6,
=6,
∴A1M2+MK2=A1K2,
∴∠A1MK=90°.

所以∠A1MK为异面直线A1M与DN所成的角.连接A1C1,AM.设正方体棱长为4,
则A1K=
 =
= ,
,MK=
 DN=
DN= =
= ,
,A1M=
 =6,
=6,∴A1M2+MK2=A1K2,
∴∠A1MK=90°.

练习册系列答案
相关题目
 .
.
 平面
平面 ;
; 棱长为2,
棱长为2,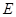 、
、 、
、 分别是
分别是 、
、 和
和 的中点.
的中点.
 面
面 ;
; 的余弦值.
的余弦值. 沿对角线
沿对角线 折起,当以
折起,当以 四点为顶点的三棱锥体积最大时,直线
四点为顶点的三棱锥体积最大时,直线 和平面
和平面 所成的角的大小为( )
所成的角的大小为( )


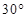
 ,则BC1与平面BB1D1D所成角的正弦值为( ).
,则BC1与平面BB1D1D所成角的正弦值为( ).




 中,
中, 、
、 分别为
分别为 、
、 的中点,则异面直线
的中点,则异面直线 与
与 所成角的余弦值为( )
所成角的余弦值为( )


 的大小是60°,线段
的大小是60°,线段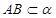 ,
, 在
在 上,
上,  与
与 所成的角为30°,则
所成的角为30°,则