题目内容
已知函数f(x)=plnx-(p-1)x2+1(1)当p=1时,f(x)≤kx恒成立,求实数k的取值范围;
(2)证明:
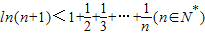 .
.
【答案】分析:(1)因为f(x)=plnx-(p-1)x2+1,所以当p=1时,f(x)≤kx恒成立,k≥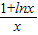 ,令
,令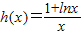 ,则k≥h(x)max,由此能求出实数k的取值范围.
,则k≥h(x)max,由此能求出实数k的取值范围.
(2)由(1)知当k=1时,lnx<x-1,令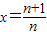 ,构造函数
,构造函数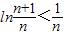 ,由此能够证明
,由此能够证明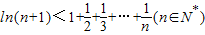 .
.
解答:解:(1)∵f(x)=plnx-(p-1)x2+1,
∴x>0,∴当p=1时,f(x)≤kx恒成立,
则1+lnx≤kx,∴k≥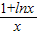 ,
,
令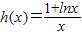 ,则k≥h(x)max,
,则k≥h(x)max,
∵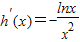 ,∴由h′(x)=0,得x=1
,∴由h′(x)=0,得x=1
且当x∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0,
所以h(x)max=h(1)=1,
故k≥1.
所以实数k的取值范围是[1,+∞).
(2)由(1)知当k=1时,有f(x)≤x,当x>1时,f(x)<x
即lnx<x-1,令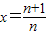 ,构造函数
,构造函数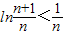 ,
,
即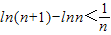 ,
,
所以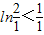 ,
,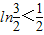 ,…,
,…,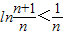 ,
,
相加得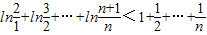 ,
,
而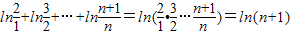 ,
,
所以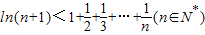 .
.
点评:本题考查函数恒成立时,实数的取值范围的求法,考查不等式的证明.解题时要认真审题,注意等价转化思想和构造法的合理运用.
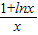 ,令
,令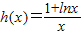 ,则k≥h(x)max,由此能求出实数k的取值范围.
,则k≥h(x)max,由此能求出实数k的取值范围.(2)由(1)知当k=1时,lnx<x-1,令
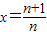 ,构造函数
,构造函数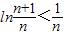 ,由此能够证明
,由此能够证明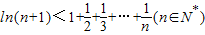 .
.解答:解:(1)∵f(x)=plnx-(p-1)x2+1,
∴x>0,∴当p=1时,f(x)≤kx恒成立,
则1+lnx≤kx,∴k≥
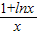 ,
,令
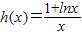 ,则k≥h(x)max,
,则k≥h(x)max,∵
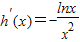 ,∴由h′(x)=0,得x=1
,∴由h′(x)=0,得x=1且当x∈(0,1)时,h′(x)>0;当x∈(1,+∞)时,h′(x)<0,
所以h(x)max=h(1)=1,
故k≥1.
所以实数k的取值范围是[1,+∞).
(2)由(1)知当k=1时,有f(x)≤x,当x>1时,f(x)<x
即lnx<x-1,令
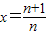 ,构造函数
,构造函数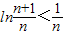 ,
,即
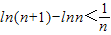 ,
,所以
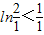 ,
,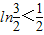 ,…,
,…,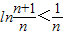 ,
,相加得
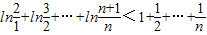 ,
,而
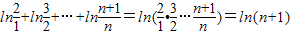 ,
,所以
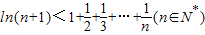 .
.点评:本题考查函数恒成立时,实数的取值范围的求法,考查不等式的证明.解题时要认真审题,注意等价转化思想和构造法的合理运用.

练习册系列答案
相关题目