题目内容
已知数列{an}满足a1=a(a为常数,a∈R),an+1=2n-3an(n∈N*),设bn= (n∈N*).
(n∈N*).
(1)求数列{bn}所满足的递推公式;
(2)求常数c、q使得bn+1-c=q(bn-c)对一切n∈N*恒成立;
(3)求数列{an}通项公式,并讨论:是否存在常数a,使得数列{an}为递增数列?若存在,求出所有这样的常数a;若不存在,说明理由.
解:(1)∵a1=a(a为常数,a∈R),an+1=2n-3an(n∈N*),
∴ ,又
,又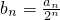 ,∴
,∴ .
.
数列bn的递推公式是 .
.
(2)∵bn+1-c=q(bn-c)(n∈N*)
∴bn+1=qbn+c-qc
又由(1)可知,
∴ ,
,
∴
(3)由(2)知,数列 是首项为
是首项为 公比为
公比为 的等比数列.
的等比数列.
∴
∴ 为所求的通项公式.
为所求的通项公式.
考察数列an,∵
1O.当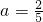 时,
时, ,
,
此时数列an是递增数列.
2O.当 时,
时,
 是正负相间出现,其绝对值是正常数
是正负相间出现,其绝对值是正常数 ,
,
而 .
.
故当n充分大时, 的值的符号
的值的符号
与 的值的符号相同,即数列的项的值是正负相间出现的,
的值的符号相同,即数列的项的值是正负相间出现的,
故数列an不可能是单调数列.
综上所述,当且仅当 时,数列an是递增数列.
时,数列an是递增数列.
分析:(1)由题意知 ,又
,又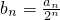 ,∴
,∴ .由此可知数列bn的递推公式.
.由此可知数列bn的递推公式.
(2)由题意知bn+1=qbn+c-qc,又由(1)可知, ,由此可知
,由此可知
(3)由(2)知,数列 是首项为
是首项为 公比为
公比为 的等比数列,由此可知
的等比数列,由此可知 为所求的通项公式.由此可求出所有这样的常数a.
为所求的通项公式.由此可求出所有这样的常数a.
点评:本题考查数列的性质及其应用,解题时要认真审题,仔细解答.
∴
 ,又
,又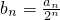 ,∴
,∴ .
.数列bn的递推公式是
 .
.(2)∵bn+1-c=q(bn-c)(n∈N*)
∴bn+1=qbn+c-qc
又由(1)可知,

∴
 ,
,∴

(3)由(2)知,数列
 是首项为
是首项为 公比为
公比为 的等比数列.
的等比数列.∴

∴
 为所求的通项公式.
为所求的通项公式.考察数列an,∵

1O.当
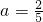 时,
时, ,
,此时数列an是递增数列.
2O.当
 时,
时, 是正负相间出现,其绝对值是正常数
是正负相间出现,其绝对值是正常数 ,
,而
 .
.故当n充分大时,
 的值的符号
的值的符号与
 的值的符号相同,即数列的项的值是正负相间出现的,
的值的符号相同,即数列的项的值是正负相间出现的,故数列an不可能是单调数列.
综上所述,当且仅当
 时,数列an是递增数列.
时,数列an是递增数列.分析:(1)由题意知
 ,又
,又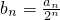 ,∴
,∴ .由此可知数列bn的递推公式.
.由此可知数列bn的递推公式.(2)由题意知bn+1=qbn+c-qc,又由(1)可知,
 ,由此可知
,由此可知
(3)由(2)知,数列
 是首项为
是首项为 公比为
公比为 的等比数列,由此可知
的等比数列,由此可知 为所求的通项公式.由此可求出所有这样的常数a.
为所求的通项公式.由此可求出所有这样的常数a.点评:本题考查数列的性质及其应用,解题时要认真审题,仔细解答.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目