题目内容
(本小题满分14分)
已知函数 ,
, .
.
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)判断函数 在区间
在区间 上零点的个数,并给予证明;
上零点的个数,并给予证明;
(Ⅲ)阅读右边的程序框图,请结合试题背景简要描述其算法功能,并求出执行框图所表达的算法后输出的 值.
值.
(1) 当 时,
时, 取得极小值
取得极小值 ,无极大值
,无极大值
(2) 函数 在区间
在区间 上有且只有一个零点.,根据构造函数思想,利用端点值函数值异号判定。
上有且只有一个零点.,根据构造函数思想,利用端点值函数值异号判定。
(3) 输出的 值为4
值为4
解析试题分析:解:(Ⅰ)∵ ,
,
 ,……………1分
,……………1分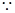 当
当 时,
时, ;当
;当 时,
时, .……………3分
.……………3分 当
当 时,
时, 取得极小值
取得极小值 ,无极大值.……………4分
,无极大值.……………4分
(Ⅱ)函数 在区间
在区间 上有且只有一个零点. ……………5分
上有且只有一个零点. ……………5分
证明如下:
∵ ,
,  ,
,  ,
, 函数
函数 在区间
在区间 上必定存在零点. ………6分
上必定存在零点. ………6分
∵ ,
, 当
当 时,
时, ,
, 
 在区间
在区间 上单调递增, 8分
上单调递增, 8分
∴函数 在区间
在区间 上的零点最多一个. ……9分
上的零点最多一个. ……9分
综上知:函数 在区间
在区间 上存在唯一零点.
上存在唯一零点.
(Ⅲ)程序框图的算法功能:找出最小的正整数 ,使
,使 的零点
的零点 满足
满足 . …10分
. …10分
∵
 ,
,  当
当 时,
时, ;
;
当 时,
时, . ……11分
. ……11分
又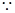
 在区间
在区间 上单调递增,
上单调递增, 当
当 时,
时, ;当
;当 时,
时, .………13分
.………13分 输出的
输出的 值为4. …………………………………14分
值为4. …………………………………14分
考点:函数极值,函数零点,框图
点评:本题主要考查函数、导数、零点、算法初步等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、数形结合思想、化归与转化思想、分类与整合思想。

练习册系列答案
相关题目
 ="12," 则输出的
="12," 则输出的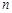 = ;
= ;
 的值是 .
的值是 .

 的值,输出相应的
的值,输出相应的 的值,
的值, 的解析式;
的解析式;
 值是____________
值是____________




