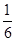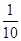题目内容
甲、乙两人练习射击, 命中目标的概率分别为 和
和 , 甲、乙两人各射击一次,目标被命中的概率为:
, 甲、乙两人各射击一次,目标被命中的概率为:
A. | B. | C. | D. |
A
解析试题分析:目标被命中包括恰好被命中一次,恰好被命中两次,再依据结论,即可;由于目标被命中包括恰好被命中一次,恰好被命中两次,则其概率为
考点:互斥事件
点评:主要是考查了互斥事件的概率的加法公式的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列叙述随机事件的频率与概率的关系中,说法正确的是( )
| A.频率就是概率 |
| B.频率是客观存在的,与试验次数无关 |
| C.随着试验次数的增多,频率越来越接近概率 |
| D.概率是随机的,在试验前不能确定 |
已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)=( )
| A.0.1588 | B.0.1587 | C.0.1586 | D.0.15858 |
某射击运动员射击所得环数ξ的分布列如下所示,则P(ξ=8)=( )
| ξ | 7 | 8 | 9 | 10 |
| P | 0.21 | m | 0.29 | 0.22 |




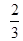 ,则阴影区域的面积为( )
,则阴影区域的面积为( )