题目内容
如图,直四棱柱ABCD—A1B1C1D1中,侧棱AA1=2,底面ABCD是菱形,AB=2,∠ABC=60°,P为侧棱BB1上的动点.
(1)求证:D1P⊥AC;
(2)当P恰为棱B1B的中点时,求四面体CPD1A的体积.
解:(1)连结BD,则AC⊥BD,

∵D1D⊥平面ABCD,∴AC⊥D1D.∴AC⊥平面BB1D1D.∵D1P![]() 平面BB1D1D,
平面BB1D1D,
∴D1P⊥AC.
(2)设BD∩AC=O,连D1O,PO,∵D1A=D1C,∴D1O⊥AC,同理PO⊥AC,
又∵D1O∩PO=O,∴AC⊥平面POD1.
∵AB=2,∠ABC=60°,∴AO=CO=1,BO=DO=![]() .
.
∴D1O=![]() =
=![]() ,PO=
,PO=![]() =2.在Rt△PB1D1中,D1P=
=2.在Rt△PB1D1中,D1P=![]() =
=![]() ,
,
在△D1OP中,cos∠D1OP=![]() =
=![]() .
.
∴sin∠D1OP=![]() =
=![]() ,
,
∴![]() =
=![]() ×
×![]() ×2×
×2×![]() =
=![]() ,
,
∴![]() =
=![]() +
+![]() =
=![]() ×
×![]() ×2=
×2=![]() .
.

练习册系列答案
相关题目
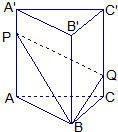 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.