题目内容
求由抛物线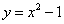 ,直线
,直线 所围成的图形的面积
所围成的图形的面积
【答案】
解 由 ,得抛物线与
,得抛物线与 轴的交点坐标是
轴的交点坐标是 和
和 ,所求图形分成两块,分别用定积分表示面积
,所求图形分成两块,分别用定积分表示面积
 ,
,
故面积 =
=
= =
=

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
题目内容
求由抛物线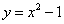 ,直线
,直线 所围成的图形的面积
所围成的图形的面积
解 由 ,得抛物线与
,得抛物线与 轴的交点坐标是
轴的交点坐标是 和
和 ,所求图形分成两块,分别用定积分表示面积
,所求图形分成两块,分别用定积分表示面积
 ,
,
故面积 =
=
= =
=

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案