题目内容
设数列{an}的前n项和为Sn,且Sn=1-(1)求证:{an}是等比数列;
(2)求Sn.
(1)证明:∵Sn=1-![]() an,
an,
∴an=Sn-Sn-1=1-![]() an-(1-
an-(1-![]() an-1)=
an-1)=![]() an-1-
an-1-![]() an,∴
an,∴![]() an=
an=![]() an-1,
an-1,
即![]() =
=![]() (n≥2).
(n≥2).
∴{an}是等比数列.
(2)解:∵a1=1-![]() a1,∴a1=
a1,∴a1=![]() ,q=
,q=![]() .∴Sn=
.∴Sn=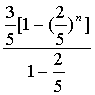 =
=![]()

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案
相关题目
题目内容
设数列{an}的前n项和为Sn,且Sn=1-(1)求证:{an}是等比数列;
(2)求Sn.
(1)证明:∵Sn=1-![]() an,
an,
∴an=Sn-Sn-1=1-![]() an-(1-
an-(1-![]() an-1)=
an-1)=![]() an-1-
an-1-![]() an,∴
an,∴![]() an=
an=![]() an-1,
an-1,
即![]() =
=![]() (n≥2).
(n≥2).
∴{an}是等比数列.
(2)解:∵a1=1-![]() a1,∴a1=
a1,∴a1=![]() ,q=
,q=![]() .∴Sn=
.∴Sn=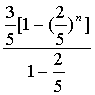 =
=![]()

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案