题目内容
已知抛物线 :
: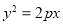 (
( )与椭圆
)与椭圆 :
: 相交所得的弦长为
相交所得的弦长为 .
.
(Ⅰ)求抛物线 的标准方程;
的标准方程;
(Ⅱ)设 ,
, 是
是 上异于原点
上异于原点 的两个不同点,直线
的两个不同点,直线 和
和 的倾斜角分别为
的倾斜角分别为 和
和 ,当
,当 ,
, 变化且
变化且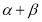 为定值
为定值 (
( )时,证明:直线
)时,证明:直线 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
10.我们把焦距和短轴相等的椭圆称为“等轴椭圆”.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,一“等轴椭圆”与该双曲线有相同的焦点,且双曲线的渐近线与椭圆相交于第一象限内的一点M,若直线F1M的斜率为$\frac{\sqrt{2}}{4}$,则该双曲线的离心率为( )
| A. | $\frac{3\sqrt{22}}{14}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{22}}{14}$或$\frac{\sqrt{6}}{2}$ |
8.有三个房间需要粉刷,粉刷方案要求:每个房间只用一种颜色,且三个房间颜色各不相同.已知三个房间的粉刷面积(单位:m2)分别为x,y,z,且x<y<z,三种颜色涂料的粉刷费用(单位:元/m2)分别为a,b,c,且a<b<c.在不同的方案中,最低的总费用(单位:元)是( )
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
10.在长方体ABCD-A1B1C1D1中,AB=$\sqrt{2}$,BC=AA1=1,点M为AB1的中点,点P为对角线AC1上的动点,点Q为底面ABCD上的动点(点P、Q可以重合),则MP+PQ的最小值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |


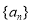 是等差数列,下列数列中仍为等差数列的有( )
是等差数列,下列数列中仍为等差数列的有( )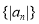 ;
;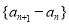 ;
;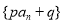 (
( ,
,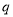 为常数);
为常数);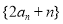 .
.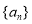 中,
中,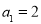 ,
,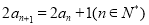 ,则
,则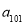 的值为( )
的值为( ) 在
在 上是增函数,则满足
上是增函数,则满足 的实数
的实数 的取值范围是______________.
的取值范围是______________.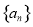 的公差为
的公差为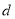 ,前
,前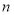 项和为
项和为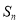 ,若
,若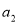 ,
,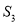 ,
,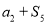 成等比数列,则
成等比数列,则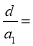 ( )
( )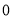 B.
B.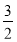
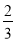 D.
D.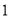
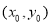 是直线
是直线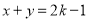 与圆
与圆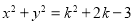 的公共点,则
的公共点,则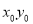 的取值范围是__________.
的取值范围是__________.