题目内容
对于函数f(x)=ax-(a+1)ln(x+1) (a>0)
(Ⅰ)试求函数f(x)的单调区间;
(Ⅱ)若a=1,数列{an}满足a1=f′(0),n≥2时,an=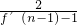 ,求证:(
,求证:(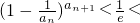
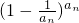 ;
;
(Ⅲ)设bn=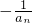 ,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010.
,Tn为数列{bn}的前n项和,求证:T2011-1<ln2011<T2010.
解:(Ⅰ)由已知的函数定义域为(-1,+∞)且f′(x)=a-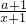 =
=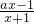 ,
,
令f′(x)=0,解得x= (a>0),
(a>0),
(i)当x∈(-1, )时,f′(x)<0,函数f(x)在(-1,
)时,f′(x)<0,函数f(x)在(-1, )内单调递增;
)内单调递增;
(ii)当x∈( ,+∞)时,f′(x)>0,函数f(x)在(
,+∞)时,f′(x)>0,函数f(x)在( ,+∞)内单调递减,
,+∞)内单调递减,
所以函数f(x)的单调减区间是(-1, ),增区间是(
),增区间是( ,+∞);
,+∞);
(Ⅱ)由已知a=1时,f′(x)=1- ,
,
∴a1=f′(0)=-1,n≥2时,an=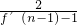 =-n,
=-n,
∴an=-n(n∈N+),
于是,所证不等式即为:
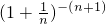 <
< <
<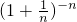 ?
?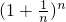 <e<
<e<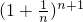 ?nln(1+
?nln(1+ )<1<(n+1)ln(1+
)<1<(n+1)ln(1+ )
)
即 <ln
<ln <
< ,
,
为此,令g(x)=x-ln(1+x)?g′(x)=1- =
= ,
,
∴当x∈(0,+∞),g′(x)>0,g(x)单调递增,又g(x)在x=0处连续,
∴n∈N+,g( )>g(0)=0?
)>g(0)=0? -ln(1+
-ln(1+ )>0,①
)>0,①
设φ(x)=ln(x+1)- ,x∈[0,+∞),
,x∈[0,+∞),
得:φ′(x)= -
-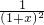 =
= ,
,
当x>0时,φ′(x)>0,所以φ(x)在(0,+∞)内是增函数,
所以φ(x)在[0,+∞)内是增函数.
当n∈N+时,φ( )>φ(0)=0,
)>φ(0)=0,
即ln(1+ )-
)-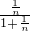 >0?
>0? <ln(1+n)②,
<ln(1+n)②,
由①②得: <ln
<ln <
< ,即
,即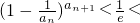
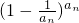 ;
;
(Ⅲ)由bn=- =
= ,则Tn=1+
,则Tn=1+ +
+ +…+
+…+ ,
,
由(Ⅱ)可知 <ln
<ln <
< ,
,
令n=1,2,3,…,2010,并将各式相加得:
 +
+ +…+
+…+ <ln
<ln +ln
+ln +…+ln
+…+ln <1+
<1+ +
+ +…+
+…+ ,
,
即T2011-1<ln2011<T2010.
分析:(Ⅰ)根据负数没有对数求出f(x)的定义域,然后求出f(x)的导函数,令导函数等于0求出x的值,在定义域内根据x的值,判断导函数的正负即可得到函数的单调区间;
(Ⅱ)把a=1代入f(x)及导函数中,确定出f(x)的导函数及f′(0)的值,进而得到an的通项,把求得的an的通项代入所证的不等式中化简,即要证 <ln
<ln <
< ,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g(
,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g( )大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)-
)大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)- ,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ(
,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ( )大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;
)大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;
(Ⅲ)把(Ⅱ)中求出的an的通项代入bn=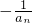 ,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.
,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.
点评:此题考查了由导函数的正负确定函数的单调区间,考查了数列与函数及不等式的综合,是一道中档题.此题的难点为第二问中不等式的证明.
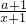 =
=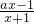 ,
,令f′(x)=0,解得x=
 (a>0),
(a>0),(i)当x∈(-1,
 )时,f′(x)<0,函数f(x)在(-1,
)时,f′(x)<0,函数f(x)在(-1, )内单调递增;
)内单调递增;(ii)当x∈(
 ,+∞)时,f′(x)>0,函数f(x)在(
,+∞)时,f′(x)>0,函数f(x)在( ,+∞)内单调递减,
,+∞)内单调递减,所以函数f(x)的单调减区间是(-1,
 ),增区间是(
),增区间是( ,+∞);
,+∞);(Ⅱ)由已知a=1时,f′(x)=1-
 ,
,∴a1=f′(0)=-1,n≥2时,an=
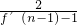 =-n,
=-n,∴an=-n(n∈N+),
于是,所证不等式即为:
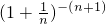 <
< <
<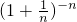 ?
?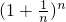 <e<
<e<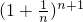 ?nln(1+
?nln(1+ )<1<(n+1)ln(1+
)<1<(n+1)ln(1+ )
)即
 <ln
<ln <
< ,
,为此,令g(x)=x-ln(1+x)?g′(x)=1-
 =
= ,
,∴当x∈(0,+∞),g′(x)>0,g(x)单调递增,又g(x)在x=0处连续,
∴n∈N+,g(
 )>g(0)=0?
)>g(0)=0? -ln(1+
-ln(1+ )>0,①
)>0,①设φ(x)=ln(x+1)-
 ,x∈[0,+∞),
,x∈[0,+∞),得:φ′(x)=
 -
-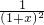 =
= ,
,当x>0时,φ′(x)>0,所以φ(x)在(0,+∞)内是增函数,
所以φ(x)在[0,+∞)内是增函数.
当n∈N+时,φ(
 )>φ(0)=0,
)>φ(0)=0,即ln(1+
 )-
)-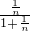 >0?
>0? <ln(1+n)②,
<ln(1+n)②,由①②得:
 <ln
<ln <
< ,即
,即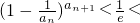
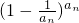 ;
;(Ⅲ)由bn=-
 =
= ,则Tn=1+
,则Tn=1+ +
+ +…+
+…+ ,
,由(Ⅱ)可知
 <ln
<ln <
< ,
,令n=1,2,3,…,2010,并将各式相加得:
 +
+ +…+
+…+ <ln
<ln +ln
+ln +…+ln
+…+ln <1+
<1+ +
+ +…+
+…+ ,
,即T2011-1<ln2011<T2010.
分析:(Ⅰ)根据负数没有对数求出f(x)的定义域,然后求出f(x)的导函数,令导函数等于0求出x的值,在定义域内根据x的值,判断导函数的正负即可得到函数的单调区间;
(Ⅱ)把a=1代入f(x)及导函数中,确定出f(x)的导函数及f′(0)的值,进而得到an的通项,把求得的an的通项代入所证的不等式中化简,即要证
 <ln
<ln <
< ,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g(
,令g(x)=x-ln(1+x),求出g(x)的导函数,找出g(x)的单调增区间为(0,+∞),又根据g(x)在x=0处连续,所以得到g( )大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)-
)大于g(0),化简后得到一个不等式,记作①,然后令φ(x)=ln(x+1)- ,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ(
,求出φ(x)的导函数,根据导函数大于0,找出φ(x)的增区间为[0,+∞),也得到φ( )大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;
)大于φ(0),代入化简后得到令一个不等式,记作②,联立①②,得证;(Ⅲ)把(Ⅱ)中求出的an的通项代入bn=
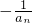 ,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.
,得到bn的通项,罗列出前n项的和Tn的各项,再根据(Ⅱ)的结论,分别令n=1,2,…,2010,代入不等式中,将各式相加,利用对数的运算法则及已知化简后,得证.点评:此题考查了由导函数的正负确定函数的单调区间,考查了数列与函数及不等式的综合,是一道中档题.此题的难点为第二问中不等式的证明.

练习册系列答案
相关题目