题目内容
a>0,当x∈[-1,1]时,f(x)=-x2-ax+b的最小值为-1,最大值为1,则实数a的值为 ________.
2 -2
-2
分析:由函数解析式得到二次函数开口向下,因此对称轴的左边是递增的,右边是递减的.因为题目中a大于0,那么对称轴- 小于0,分-
小于0,分- 小于-1和-
小于-1和- 小于0大于等于-1两种情况考虑,分别找出函数的最大值和最小值,根据已知的最小值为-1,最大值为1,列出关于a与b的两个方程,联立即可求出a的值,经过检验即可得到满足题意的a的值.
小于0大于等于-1两种情况考虑,分别找出函数的最大值和最小值,根据已知的最小值为-1,最大值为1,列出关于a与b的两个方程,联立即可求出a的值,经过检验即可得到满足题意的a的值.
解答:由f(x)=-x2-ax+b,得到对称轴为直线x=- ,由a>0得到-
,由a>0得到- <0,
<0,
当- <-1即a>2时,得到函数f(x)的最小值为f(1)=-1-a+b=-1,即a=b①;
<-1即a>2时,得到函数f(x)的最小值为f(1)=-1-a+b=-1,即a=b①;
最大值为f(-1)=-1+a+b=1,即a+b=2②,把①代入②解得:a=1与a>2矛盾;
当-1≤- <0即0<a≤2时,得到函数的最大值为顶点纵坐标
<0即0<a≤2时,得到函数的最大值为顶点纵坐标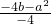 =1,化简得:a2+4b-4=0①;
=1,化简得:a2+4b-4=0①;
最小值为f(1)=-1-a+b=-1,即a=b②,由②代入①得:a2+4a-4=0,解得:a=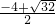 =-2+2
=-2+2 ,a=-2-2
,a=-2-2 (舍去),
(舍去),
综上,实数a的值为2 -2.
-2.
故答案为:2 -2
-2
点评:此题考查了二次函数的图象与性质,考查了分类讨论的数学思想,是一道综合题.最值在哪一点取得是解题的关键,而最值的取得和对称轴的位置有关,因此题目分类讨论的基准就是对称轴和区间[-1,1]的位置关系.
 -2
-2分析:由函数解析式得到二次函数开口向下,因此对称轴的左边是递增的,右边是递减的.因为题目中a大于0,那么对称轴-
 小于0,分-
小于0,分- 小于-1和-
小于-1和- 小于0大于等于-1两种情况考虑,分别找出函数的最大值和最小值,根据已知的最小值为-1,最大值为1,列出关于a与b的两个方程,联立即可求出a的值,经过检验即可得到满足题意的a的值.
小于0大于等于-1两种情况考虑,分别找出函数的最大值和最小值,根据已知的最小值为-1,最大值为1,列出关于a与b的两个方程,联立即可求出a的值,经过检验即可得到满足题意的a的值.解答:由f(x)=-x2-ax+b,得到对称轴为直线x=-
 ,由a>0得到-
,由a>0得到- <0,
<0,当-
 <-1即a>2时,得到函数f(x)的最小值为f(1)=-1-a+b=-1,即a=b①;
<-1即a>2时,得到函数f(x)的最小值为f(1)=-1-a+b=-1,即a=b①;最大值为f(-1)=-1+a+b=1,即a+b=2②,把①代入②解得:a=1与a>2矛盾;
当-1≤-
 <0即0<a≤2时,得到函数的最大值为顶点纵坐标
<0即0<a≤2时,得到函数的最大值为顶点纵坐标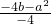 =1,化简得:a2+4b-4=0①;
=1,化简得:a2+4b-4=0①;最小值为f(1)=-1-a+b=-1,即a=b②,由②代入①得:a2+4a-4=0,解得:a=
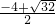 =-2+2
=-2+2 ,a=-2-2
,a=-2-2 (舍去),
(舍去),综上,实数a的值为2
 -2.
-2.故答案为:2
 -2
-2点评:此题考查了二次函数的图象与性质,考查了分类讨论的数学思想,是一道综合题.最值在哪一点取得是解题的关键,而最值的取得和对称轴的位置有关,因此题目分类讨论的基准就是对称轴和区间[-1,1]的位置关系.

练习册系列答案
相关题目