题目内容
(本题满分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足![]() 。
。
(Ⅰ)求角C的大小;
(Ⅱ)求![]() 的最大值。
的最大值。
解析本题主要余弦定理、三角形面积公式、三角变换等基础知识,同时考查三角运算求解能力。
(Ⅰ)解:由题意可知
![]() absinC=
absinC=![]() ,2abcosC.
,2abcosC.
所以tanC=![]() .
.
因为0<C<![]() ,
,
所以C=![]() .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin(![]() -C-A)=sinA+sin(
-C-A)=sinA+sin(![]() -A)
-A)
=sinA+![]() cosA+
cosA+![]() sinA=
sinA=![]() sin(A+
sin(A+![]() )≤
)≤![]() .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是![]() .
.

练习册系列答案
相关题目
 BAD=90°,PA
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.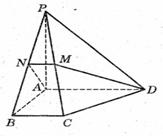
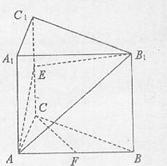
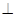 底面ABCD,
底面ABCD,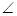 DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.
DAB为直角,AB‖CD,AD=CD=2AB,E、F分别为PC、CD的中点.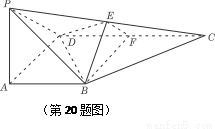
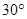 ,求k的取值范围.
,求k的取值范围. .
.