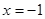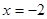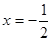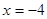题目内容
设抛物线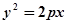 的准线
的准线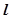 ,焦点为
,焦点为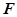 ,顶点为
,顶点为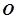 ,
,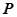 为抛物线上任意一点,
为抛物线上任意一点,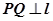 ,
,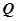 为垂足,求
为垂足,求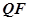 与
与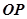 的交点
的交点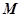 的轨迹方程.
的轨迹方程.
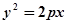 的准线
的准线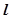 ,焦点为
,焦点为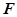 ,顶点为
,顶点为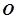 ,
,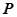 为抛物线上任意一点,
为抛物线上任意一点,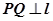 ,
,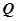 为垂足,求
为垂足,求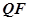 与
与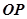 的交点
的交点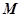 的轨迹方程.
的轨迹方程.交点M的轨迹方程 .
.
 .
.本小题属于相关点法求轨迹方程,可以引进参数t,设 ,然后分别求出直线
,然后分别求出直线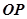 的方程和直线
的方程和直线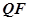 的方程,再联立解方程组可得到动点M的参数方程,消去参数t就得到动点M的轨迹方程.
的方程,再联立解方程组可得到动点M的参数方程,消去参数t就得到动点M的轨迹方程.
解:设抛物线上点 ,直线
,直线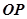 的方程为:
的方程为: .
.
又 ,
, , ∴直线
, ∴直线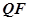 的方程
的方程 .它们的交点
.它们的交点 ,
,
由方程组 由①×②得:
由①×②得: ,
,
∴交点M的轨迹方程 .
.
直接法也是可以做的,不同的设法也是可以解决的.
 ,然后分别求出直线
,然后分别求出直线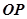 的方程和直线
的方程和直线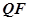 的方程,再联立解方程组可得到动点M的参数方程,消去参数t就得到动点M的轨迹方程.
的方程,再联立解方程组可得到动点M的参数方程,消去参数t就得到动点M的轨迹方程.解:设抛物线上点
 ,直线
,直线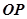 的方程为:
的方程为: .
.又
 ,
, , ∴直线
, ∴直线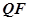 的方程
的方程 .它们的交点
.它们的交点 ,
,由方程组
 由①×②得:
由①×②得: ,
,∴交点M的轨迹方程
 .
.直接法也是可以做的,不同的设法也是可以解决的.

练习册系列答案
相关题目
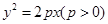 的焦点F作倾斜角为
的焦点F作倾斜角为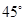 的直线交抛物线于A、B
的直线交抛物线于A、B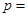 ________________
________________ 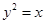 的焦点为F,点M在抛物线上,线段MF的延长线与直线
的焦点为F,点M在抛物线上,线段MF的延长线与直线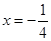 交于点N,则
交于点N,则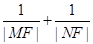 的值为
的值为 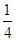

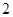
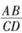 -的值越大,P越大;
-的值越大,P越大;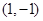 为中点的抛物线
为中点的抛物线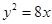 的弦所在直线方程为: .
的弦所在直线方程为: .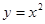 上到直线
上到直线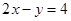 距离最近的点的坐标是______ ___.
距离最近的点的坐标是______ ___.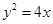 的焦点
的焦点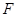 的直线交抛物线于
的直线交抛物线于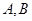 两点,点
两点,点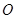 是原点,若
是原点,若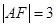 ;则
;则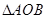 的面积为( )
的面积为( )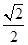
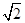
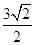
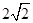

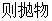
 ( )
( )