Question

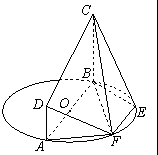如图，AB为圆O的直径，点E、F在圆O上，AB∥EF，直角梯形ABCD所在的平面和圆O所在的平面互相垂直，∠CBA=90°，AB=BC=2，AD=EF=1．
（1）证明：AF⊥平面CBF；
（2）设平面CBF将几何体EFABCD分成的两个锥体的体积分别为V_F-ABCD、V_F-CBE，求V_F-ABCD：V_F-CBE．

Answer 1

解：（1）∵平面ABCD⊥平面ABEF，平面ABCD∩平面ABEF=AB，CB⊆平面ABCD，CB⊥AB，
∴CB⊥平面ABEF，（2分）
∵AF⊆平面ABEF，AF⊥BC．（3分）
∵AB为圆O的直径，∴AF⊥BF，（4分）
又∵CB∩BF=B，
∴AF⊥平面CBF．（6分）
（2）过点F作FG⊥AB于G，
∵平面ABCD⊥平面ABEF，平面ABCD∩平面ABEF=AB，FG⊆平面ABEF，FG⊥AB，
∴FG⊥平面ABCD，
∴V_F-ABCD=××（1+2）×2×FG=FG，（8分）
而V_F-BCE=V_C-BEF=S_△BEF×CB=××FG×2=FG，（10分）
由此可得V_F-ABCD：V_F-CBE=3：1（12分）
分析：（1）根据面面垂直的性质，结合题意可证出CB⊥平面ABEF，从而有AF⊥BC，由圆直径的性质得到AF⊥BF，再根据线面垂直的判定定理，得到AF⊥平面CBF．
（2）过点F作FG⊥AB于G，可得FG即为四棱锥F-ABCD的高，用锥体体积公式结合题中数据可算出四棱锥F-ABCD的体积为FG，再用体积转换算出三棱锥F-CBE的体积为FG，从而得到四棱锥F-ABCD与三棱锥F-CBE的体积之比．
点评：本小题主要考查立体几何的相关知识及空间想象能力，具体应用到线面垂直的判定定理与面面垂直的性质定理以及体积求法等知识，属于中档题．